Experimental work on the Equivalence Principle is closely
associated with the name of Loránd (or Roland) Eötvös (1848-1919). In
addition to his work on gravitational problems, he was also a pioneer
in the fields of capillarity and geomagnetism. His version of the
torsion balance was a conceptually simple but very carefully planned,
manufactured, and tested device. He improved the limits on any
deviation from the proportionality of inertial and gravitational
masses by almost four orders of magnitude - first around 1888 by a
factor of 400, then between 1905 and 1908 by another factor of about
ten. He also measured the value of the universal gravitational
constant G with high precision, and put stringent limits on any
screening of the gravitational force by intervening material. His
extensive field work in gravitational gradiometry served as a model
for precision measurements both in geophysics and in geodesy.
Although he always concentrated on basic research, his instruments
and methods later proved of vital importance for prospecting for oil
and natural gas. Several of the objectives of the STEP mission are
closely related to problems that Baron Loránd Eötvös discussed and
examined about hundred years ago.
Loránd Eötvös - or Vásárosnaményi Báró Eötvös Loránd by full
Hungarian name - who is better known abroad by the Germanized form
of his name as Roland von Eötvös, was born in 1848, the year of the
Hungarian revolution. He was the son of a well-known poet, writer,
and liberal politician, who was cabinet minister at the time, and
played an important part in 19th century Hungarian intellectual and
political life. Loránd Eötvös first studied law, but soon switched
over to physics and went abroad to study in Heidelberg and Königsberg.
After his doctorate he became a university professor in Budapest very
soon, and played a leading part in Hungarian science for almost half
a century. He gained international recognition first by his
innovative work on capillarity, then by his refined experimental
methods and extensive field studies in gravity. He died in 1919, but
his last and probably most important paper, written together with his
colleagues D. Pekár and J. Fekete, was published only in 1922.
Eötvös started to experiment with gravity and the torsion balance around 1885. His first instruments were similar to those of Mitchell, Cavendish, and Coulomb, and served mainly for demonstration purposes. The torsion balance was at that time a horizontal rod suspended at the centre. Eötvös soon realized the potentialities of this simple device for measuring the difference between the two main curvatures of the very local equipotential surface, i.e. of the surface perpendicular in each point to the combined effects of gravity and the centrifugal force due to earth rotation. By 1890 he was able to measure the mass of the Gellért-hill in Budapest, and had also finished his first test on the Equivalence Principle.
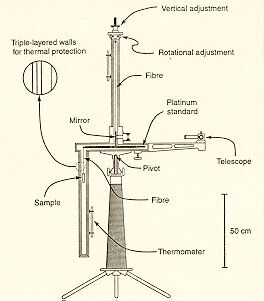
A new version of the torsion balance having one weight hanging down
from the end of the rod got ready in 1991. This was called horizontal
variometer by Eötvös, because it made it possible to measure the horizontal
gradient of g in addition to the direction and difference of the two
main curvatures. This is the instrument generally known as Eötvös
balance. It was used for extensive field measurements and later for
prospecting for oil and natural gas. A sketch of the simple balance
is shown below after Fischbach and Talmadge (Nature 356, 207, 1992).

While Eötvös dedicated most of his time and ingenuity to improving the precision and stability of the torsion balance, he also developed several other innovative instruments. Although some of them still exist as museum exhibits, the detailed description of most of them was never published, because either he wanted to further improve them, or his attention was diverted by some new project. He was often in a situation reminiscent of his predecessor in the Chair of Experimental Physics of Budapest University, Ányos Jedlik, who invented and constructed both the electric motor and the dynamo probably years before anyone else, and also used them in his laboratory, but for a long time told practically nobody about them.
Some of the instruments of Eötvös were mainly intended for demonstrating important laws like the mutual attraction of massive bodies, while others were more for research. He extensively used resonance to increase sensitivity. For instance a small motor was used to periodically displace masses first to one, then to the other side of a torsion balance. When this displacement was in resonance with the natural torsional oscillations, sensitivity increased dramatically. He called this device gravitational multiplyer. He also started to experiment with bifilar gravimeters in the 1890's, but finally was not satisfied with their reliability. A torsion balance rotating around a horizontal axis for measuring the vertical gradient of g was also abandoned later. His magnetic instruments had high sensitivity and were used for routine measurements during his gravitational surveys. They were sensitive enough to measure paleomagnetic and archeomagnetic effects. He presented a talk on that subject as early as in 1900.
One of his most inventive devices was the so-called gravitational
compensator. The major obstacle in the way of increasing the
sensitivity of the torsion balance was that the fibre had to be
strong enough to hold the weight, but then its restoring torque was
very hard to reduce. Eötvös used rotatable massive lead sectors to
arbitrarily reduce the effective restoring torque by changing the
very local gravity field, thus achieving in principle an arbitrarily
large sensitivity.
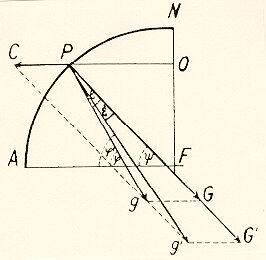
It is not quite clear what motivated Eötvös for starting a series of experiments on the proportionality of inertial and gravitational masses. He certainly recognized both the importance of that principle for Newtonian mechanics and the fact that previous experimental evidence was very limited, but it was probably only when he realized the huge capabilities of his instrument that he decided to go ahead. It was a very subtle idea that any deviation from the proportionality of gravitating and inertial masses could be best checked by detecting tiny differences in the direction of the acceleration of different substances, and that those differences might be detected by rotations of a horizontal rod. He succeeded in improving the precision of the careful pendulum experiments of Bessel by a factor of 400. The curvature variometer with both of its weights at the same height - his only torsion balance at the time - is in fact in principle better for that purpose than the Eötvös balance used in the EPF experiments between 1905 and 1908. The factor of ten increase of precision in the latter experiment can be ascribed to the technical improvement of the balance and to more careful experimental methods.
The small deviation in the direction of accelerations he was able to
detect sounds still formidable (1/60000 arc second in those early
measurements!). The EPF experiment was extensively discussed and
became widely known during the last seven years due to the Fifth
Force suggestion of E. Fischbach et al. (Reanalysis of the
Eötvös Experiment, Phys.Rev.Lett. 56,3, 1986), and there is too
little space to add any discussion here. I rather include a fairly
well-known sketch of Eötvös as a reminder of the principles of the
measurements. It shows what the combined effects of gravity and centrifugal force (due
to Earth rotation) would be for two bodies made of different substances,
having the same inertial mass, but slightly different gravitational
masses.
Before turning to gravity, Eötvös achieved his most important results in the field of capillarity. The generality and simplicity of the Eötvös law in that field ranks with the universal gas laws. Without going into details, we note some analogies between his methods in both fields. First he devised a very sensitive method based on optical reflection to study the local geometry of the surface. But the properties of the surface changed in time - so he enclosed the fluid in a closed glass tube, and stability was achieved. Then he could study the changes in the differential geometry of the surface as he heated the fluid up to the critical temperature. The fluid surface is determined by very short-range forces while the forces defining the equipotential surfaces of gravity are long-range ones, but some of the methods to describe and measure them are surprisingly similar.
In the field of gravity, his measurements of G should be mentioned. First he used the Cavendish method, but optimized the position of the attracting mass so that the dependence on positional uncertainty should be minimum. Later he used various static and dynamical methods. One of his measurements involved a suspended horizontal rod between two massive lead columns. Oscillation times were measured for equilbrium positions both parallel and perpendicular to the separation of the lead columns (640 and 860 s respectively). Then the lead columns were removed, and the measurements reiterated. There was still some difference due to inhomogeneities of the local gravitational field, but that latter measurement could now be used for correction. A relative precision in G of 1/500 was achieved.
He also tried to measure whether gravity can be shielded. Again
several methods were used. One involved the gravitational
compensator. The results showed that even for a lead plate as thick
as the earth diameter, the screening cannot exceed 1/800 of the force.
It was noted that under quiet condition a much better precision could
be achieved. Another ingenious measurement used the Eötvös balance
aligned with the meridian at sunset or sunrise. If one of the weights
is 1 m lower than the other, gravity should penetrate several km of
earth to reach the low weight, while there is no intervening material
for the high one. No rotation of the balance was noted.
The Eötvös balance was the first instrument for gravitational gradiometry, that is for the measurement of the very local properties of the shape of the equipotential surfaces of earth. Eötvös started his measurements by mapping the second derivatives of the potential in several points of his room, then of his whole Institute. Local masses substantially influence those values. Eötvös also tried to estimate what those derivatives would be if the building was not there, and he arrived at a value surprisingly close to the results of modern measurements. With the Eötvös balance four of the five independent second derivatives are measured, while with the curvature variometer only two.
Relatively slow motions of massive bodies or fluid masses can also be followed by the changes in the shape of potential surfaces as detected by the Eötvös balance. The sensitivity for such changes can be increased by the use of the gravitational compensator, although in practice very few such measurements were done. Changes in the water level of the Danube could allegedly be detected from a cellar 100 m away with a cm precision, but that measurement was not well documented. There were also plans to make mesurements at Vesuvius, where the upsurge of the magma could in principle be detected at a depth of several km. Of course seismic noise might make that high precision illusory.
An interesting set of Eötvös balance measurements was done in 1910 in a valley between Monte Cristallo and Croda Rossa in the Dolomites, near Schluderbach (Carbonin). Due to the influence of the high mountains on both sides, the radius of curvature perpendicular to the axis of the valley turned out to be 200000 km, i.e. about 30 times more than the normal value of about one earth radius. The arrangement of nearby masses was similar to a giant gravitational compensator.
In honour of Eötvös, a convenient unit for gradiometry
( 10-9
s-2 ) was named after him.
Although Eötvös was always interested in the implications and possible applications of his and his collaborators' measurements, he preferred not to rush to conclusions. He realized that the relationship between his results and the arrangement of underground density distributions was a rather complicated one. Some general principles like isostasy could be relatively easily checked, but for most of his working life he considered his results more as scientific achievements and less as a kind of prospecting. He was quite aware of the signatures which might mean oil or natural gas, and also made some calculations for such situations, but his expeditions usually had other preferences.
The first strong correlation between results of measurements made with his instrument and actually finding oil was at Egbell (now Slovakia), which is often considered as the birth of applied geophysics. After the death of Eötvös, his balance was extensively used for prospecting in many countries of the world, and proved to be very efficient under certein geological circumstances, such as in Texas. Eötvös balances were produced in large numbers, and several improvements were made to make the work more convenient under difficult circumstances such as in mines.
Subterranean perturbations of the gradients and directive forces of gravity were measured by Eötvös on the ice sheet of lake Balaton in 1901 and 1903. The torsion balance observations were done on a frozen lake in order to minimize disturbances of topographic origin. Some underground mountain-like formations were discovered. Afterward, he wrote: My unknown country spread out far below the frozen surface of lake Balaton. I have never seen it and shall never see it, only my instrument sensed it, still how hard it was to part with it when the ice started to melt."
The Geophysical Institute in Budapest, the Budapest University, and
the Hungarian Physical Society are named after Baron Loránd Eötvös.
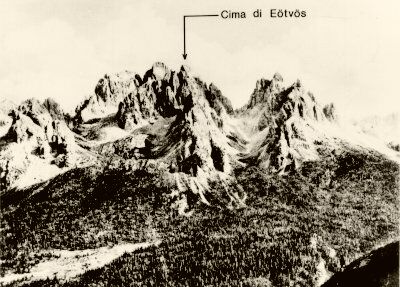
Mountaineering, rock-climbing, and (mainly stereoscopic) photography
were among the favourite passtimes of Eötvös. He was chairman of the
Budapest branch of the Carpathian Association, later of the Hungarian
Mountaineering Federation. He spent most of his summers in
Schluderbach (now Carbonin) in the Dolomites. With his daughters he
made the first ascent of several peaks and access routes in that
region. One of the peaks in the Cadin range near Cortina d'Ampezzo
was even named after him. Even at the age of 68, shortly before his
death, he climbed some of the highest peaks of the Tatra mountains.
He was also deeply impressed by the 'underground mountains' never
seen by man, but clearly detected by his sensitive instrument
underneath lake Balaton and the Hungarian Plains.
J. Eötvös, the father of R. Eötvös was a well-known poet, writer, and politician. R. Eötvös also inherited some of his talents and wrote several poems in his youth, and always held both poets and scientists in high esteem. Two of his quotes on their respective values:
"Poets can penetrate deeper into the realm of secrets than scientists."
"A scientist can soar high like a poet, but also knows how high he flies."
The following short poem written by the young Eötvös (quoted in
Hungarian and German in the Foreword by the Editor to his Collected
Works, 1953) shows his youthful ambitions, and might gain added
relevance should STEP be renamed Eötvös.
Laurels beckoned us, so we started out
With Nightingale towards a mountain height.
While I grappled with the sheer cliffs below,
She seized her prize in easy, graceful flight.
What I may perhaps never ever reach,
Took but a brief moment for the bird;
O Heaven don't be so unjust, I plead,
Grant me wings too. Let my prayer be heard.
In view of the important contributions of Baron R. Eötvös to the fundaments of each of the main fields of research where the STEP project intends to achieve dramatic improvements, I suggest to the STEP community to consider a change of name of the mission to Eötvös. The main arguments supporting that suggestion are as follows.
1. The new, extended scope of the mission is no more properly described by the acronym STEP standing for the Satellite Test of the Equivalence Principle. In addition, STEP is also the acronym for the Solar Terrestrial Energy Program, and is used as an abbreviation of Solar TErrestrial Physics as e.g. in SCOSTEP.
2. The name of Baron R. Eötvös is equally well known in the fields of fundamental gravity research, in geodesy (where an important unit is named after him), and in pure and applied geophysics. Named missions have recently gained ground for emphasizing a mission's heritage.
3. The recent Fifth Force suggestion by E. Fischbach et al. that gave new impetus to experimental gravity research was based on a reanalysis of the 80-year old Eötvös-Pekár-Fekete (EPF) experiment, showing that the methods and ideas of Eötvös have relevance even today.
This short paper summarises the achievements of Eötvös in physics
and geophysics. It was presented as a poster at the STEP (Satellite Test
of the Equivalence Principle) Symposium in Pisa, 6-8 April 1993, and
published, without figures, in the Proceedings volume (esa WPP-115,
July 1996, pp 399-406; Editor R. Reinhard, ESTEC, Noordwijk, The Netherlands)
 |