Bárdos László, fizikatanár <l-aci@freemail.hu>
Apáczai Csere János Elméleti Líceum -
Kolozsvár
ELŐSZÓ
E dolgozat megírását az tette szükségszerűvé, hogy a fizikaórán
elméleti és kísérleti úton szerzett ismereteket számítógépes környezetben interaktív
módon lehessen elmélyíteni. Az interaktivitást a KSEG vektorgrafikai
program biztosítja.(Windowsos változat letöltése
itt, Linux vagy Mac OS X változatok innen
tölthetők le.)
A mai korosztály egyre inkább a vizuális ismeretszerzésre
hagyatkozik. A fogalmi gondolkodása, ami olvasással fejleszthető, háttérbe szorul.
Számukra nagy segítséget jelentenek a vizuális modellek. Az origami példázatán
megérthetjük miért is van akkora szükség a vizuális modellekre. Origami esetében,
ha nem látjuk magát a hajtogatást csak egyszerű szöveges leírást kapunk, többségünk
nem lesz képes a modellt megalkotni, viszont ha előttünk hajtogatja valaki,
akkor viszonylag könnyen megoldjuk a feladatot.
Az ismeretszerzés aktív módszereken keresztül a leghatékonyabb. A fizikaórán
a kísérletezés a legaktívabb és legeredményesebb módszer.
A geometriai optika oktatásában a tanár többnyire frontális kísérleteket végez,
ilyenkor a diák passzívabb módon jut ismeretekhez mint egyéni kísérletezéssel.
Azokban az iskolákban, ahol nincs fizika laboratórium, vagy a használata korlátozott
a kevés tanterem vagy a sok párhuzamos osztály miatt, egyéni kísérletezésre
még kevesebb az esély. Egyik megoldás az lenne tehát, hogy számítógépes, interaktív
környezetben, akár otthon is megismételhesse az aktív modellek révén a fényjelenségek
törvényszerűségeit, a képalkotást a képalkotó eszközökön keresztül. Számos internetről
letölthető programocska, honlapokba beágyazott applet igyekszik ezt a hiányt
pótolni. Egyedüli szépséghibájuk, hogy zárt kódjuk van, tovább nem fejleszthetőek,
vagy éppenséggel idealizált modellek. A KSEG-ben modellezett jelenségek ezekkel
ellentétben továbbfejlesztésre alkalmasak, a program használata pedig gyorsan
elsajátítható.
Ajánlom a geometriai fénytan vektorgrafikai modelleken keresztüli
alkalmazását mindazoknak, akik az optikai jelenségek mélyére
szeretnének „látni”.
A dolgozat megírásában és tovább gondolásában nyújtott útmutatásokért köszönettel
tartozom dr. Néda Zoltán egyetemi tanárnak.
I. BEVEZETÉS
A geometriai optika egyaránt alapja az absztrakt kutatásnak valamint a mérnöki
tervezésnek, fejlesztésnek. Mivel viszonylag rég kialakult tudományága a fizikának
sokak által lezártnak tekintett.
Tartalma, lényege kevés, hiszen egyetlen elvből a Fermat-elvből lényege levezethető,
mindamellett végtelen mert következményeinek, alkalmazásainak tárháza szinte
kimeríthetetlen.
*
A fény- a legtöbb életforma számára nélkülözhetetlen. Szimbóluma
ősidők óta a tudásnak, szivárványként szövetségnek a divinitással, villámként
Isten haragjának, Napkultuszoknak. Kedélyállapotunk jellemzésére használt szavaink
is vele kapcsolatosak: derűs, felhőtlen, borús.
A látás legfontosabb megismerési csatornánk. A környezetünket folyamatosan látással
pásztázzuk, letapogatjuk, azaz tájékozódunk. A változásokról leggyorsabban és
legpontosabban általa értesülünk, mivel terjedési sebessége határsebesség és
az információ általa torzul talán a legkevésbé. Az állatvilágban a látás a legfontosabb
érzékelési csatorna. Szerepe van a tájékozódásban, táplálékszerzésben, társkeresésben,
menekülésben. A makrokozmosztól a mikrokozmoszig értelmezhetünk segítségével.
1.1 A geometriai fénytan rövid
történeti áttekintése.
Ókor.
Már az ókori görögök, arabok, kínaiak elméleteket
dolgoztak ki a fénnyel és látással kapcsolatosan.
Bár túlnyomórészt hibások voltak, mégis
évezredeken keresztül fennmaradtak. Helyesen állapították
meg, hogy vannak maguktól világító testek, illetve
olyanok, amelyek láthatóságához meg kell világítani
őket. A látás mechanizmusáról Püthagorasz
és Empedoklész
úgy vélekedtek, hogy a tárgy és a szem is egyaránt
kibocsát „valamit” és ezek találkozásakor
lesz észlelhető a tárgy. Manapság a képalkotó
eszközök (fényképezőgép, kamera, stb.)
egyértelművé tették, hogy a fénykibocsátáshoz
a szem nem szükséges. Eukleidész
i.e. 300 körül megteremti a geometriai optikai alapjait, fénytani
tárgyú fő művei: Optika, Katoptrika (tartalmazza
a fényvisszaverődés törvényét). Arkhimédész
(i.e. 230), a legenda szerint tükreivel felgyújtotta a Szirakuzát
támadó római flotta hajóit. Héron (62): a
fény útja visszaverődéskor minimum feltételeket
elégít ki.
Középkor.
Al-Kindi
(813–873): a szem működését tanulmányozta;
fénytani összefoglalója Keplerig egyetemi tankönyv volt.
Alhazen
(965?–1040/1041) a fénytörés síkját helyesen
értelmezte, vizsgálta a szem és a camera obscura működését,
tanulmányozta a gömb és parabola tükrök képalkotásának
elméletét. Al-Sirazi
megállapítja, hogy a szivárvány keletkezését
a fénytörés és fényvisszaverődés
okozza. Roger Bacon (1220?–1292?)
a homorú gömbtükröket tanulmányozta, megmérte
fókusztávolságukat, kimutatta a szférikus aberrációt
és megállapította, hogy parabola tükröknél
ez a hiba nem jelenik meg.
Reneszánsz.
Leonardo
Da Vinci (1452–1519) megállapította,
hogy fénytöréskor a beesési és törési
szögek szinuszainak hányadosa állandó. Galilei
1609-től korának legjobb távcsöveit
készíti. 1612-ben mikroszkópot is készít.
Elkészülnek Niccolo
Zucchius, Newton
és Cassegrain
tükrös távcsövei. Leeuwenhoek
(1632-1723) a mikroszkópról könyvet ír. Snellius
(1591–1626) 1620-ban megállapítja a fénytörés
törvényét, de Descartes
publikálja először 1637-ben. Pierre
de Fermat (1601–1665): Fermat-elv.
Azt, hogy milyen sebességgel terjed a fény Galilei
sikertelenül próbálta megmérni. Egyik toronyban ő állott, egy távoli másik toronyban
egy társa. Amikor Galilei felkapcsolta a lámpáját, a társa
amint észrevette, maga is felkapcsolta a sajátját. Az időeltolódás a reakcióidőhöz
képest elhanyagolható volt. Newton is úgy vélekedett, hogy
a távolhatások azonnaliak, a fény terjedési sebességét sem tekintették végesnek.
Olaf
Christensen Römer (1676) dán csillagász mérte
elsőként meg a fény terjedési sebességét.
A Jupiter holdjainak a Jupiter árnyékában eltöltött
idejét mérte egymást követő eklipszisekre és 7 perces eltérést
kapott a Föld – Jupiter közötti különböző távolságoknak
megfelelően. Ebből arra következtetett, hogy azért
van a 7 perces késés, mert a fény nagyobb távolságból
később érkezik, tehát a fényterjedés sebessége véges.
Mivel a Föld-pálya sugarára is csak becslés volt akkoriban,
a mért érték körülbelül 2.108 m/s, a ma
ismertnél 30%-kal volt kisebb.
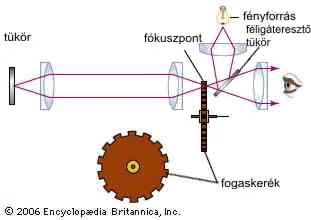 Az első pontos méréseket, földi tárgyakat igénybe véve, Fizeau
végzi 1849-ben. A méréshez négy lencsét, két síktükröt (az egyik féligáteresztő) és egy fogaskereket használt. A baloldali tükör a fényutat megduplázza (16 km),
a lencsék párhuzamosítják a nyalábot illetve fokalizálják két fog közötti hézagra.
A féligáteresztő tükrön és a párhuzamosító okulárlencsén keresztül szemlélik
a távoli tükörről visszaverődő nyalábot. A fogaskerék sebességét addig növelik,
amíg a visszaverődő nyaláb nem jut a szembe, mert elárnyékolja az elébe kerülő
fog. Ezt a forgási sebességet a duplájára növelve, lesz a legnagyobb a szembe
jutó fényáram, mert a következő hézagon keresztül a visszavert nyaláb egészében
eljut a megfigyelő szemébe. E módszerrel a fény sebességére kapott érték 315
000 km/s volt.
Az első pontos méréseket, földi tárgyakat igénybe véve, Fizeau
végzi 1849-ben. A méréshez négy lencsét, két síktükröt (az egyik féligáteresztő) és egy fogaskereket használt. A baloldali tükör a fényutat megduplázza (16 km),
a lencsék párhuzamosítják a nyalábot illetve fokalizálják két fog közötti hézagra.
A féligáteresztő tükrön és a párhuzamosító okulárlencsén keresztül szemlélik
a távoli tükörről visszaverődő nyalábot. A fogaskerék sebességét addig növelik,
amíg a visszaverődő nyaláb nem jut a szembe, mert elárnyékolja az elébe kerülő
fog. Ezt a forgási sebességet a duplájára növelve, lesz a legnagyobb a szembe
jutó fényáram, mert a következő hézagon keresztül a visszavert nyaláb egészében
eljut a megfigyelő szemébe. E módszerrel a fény sebességére kapott érték 315
000 km/s volt.
Ernst Abbe (1840-1905) megállapítja
a mikroszkóp feloldóképességének képletét.
1.2 Az optikai eszközök szerepe a tudományos megismerésben
A szemünk majdnem tökéletes optikai eszköz, de feloldóképessége
nem haladja meg a 0,01 mm-t. Szabad szemmel nem tudjuk megfigyelni a mikroszkopikus
méretű élőlényeket (baktériumok, vírusok, protozoák), de a gigantikus méretű
nagyon távoli testekkel is hasonlóan vagyunk. A Tejút-rendszert alkotó távoli
csillagokat például ködszerű, elmosódott halmazként látjuk. Az evolúció a közvetlen
környezetünk értelmezésének megfelelő képalkotó eszközt eredményezett. Azokat
a mikroszkopikus dolgokat, lényeket, amelyekről tudjuk, hogy sok esetben betegségeink
forrásai lehetnek, ha láttuk volna sem lettünk volna képes befolyásolni. A tudomány
adta kezünkbe az eszközöket, amelyekkel az addig láthatatlan világ feltárhatóvá,
értelmezhetővé vált.
Az egyik ilyen eszközünk a mikroszkóp,
a másik a teleszkóp. Előbbivel a közvetlen
környezetünkben levő parányi méretű tárgyak világát, a mikrokozmoszt, utóbbival
a végtelennek tűnő világegyetemet tanulmányozhatjuk.
Antonie van Leeuwenhoek (1677)
lencsecsiszoló figyelt meg elsőként saját készítésű egylencsés mikroszkópján
mikroszkopikus élőlényeket. Ezt nevezhetjük tehát a mikrobiológia első állomásának.
A mikrobiológia megteremtődése mérföldkő a modern gyógyászat tekintetében. Gyógyszerkészítmények,
oltások az utóbbi száz év alatt csaknem megduplázták a várható élettartamot.
A teljes fényvisszaverődés elvét hasznosító eszközzel, az endoszkóppal szó szerint
beleláthatunk az ember belsejébe és sok esetben diagnosztizálhatunk sebészi
beavatkozás nélkül.
A Ptolemaioszi
geocentrikus világkép csaknem két évezredes fennállása a távcsövek felfedezésével
ért véget, helyét a Kopernikuszi
heliocentrikus világkép foglalta el. A távcső a csillagászat legfontosabb eszköze.
A távcsövek fényt derítettek a Naprendszer mozgástörvényeire, a Tejút méreteire,
csillagainak számára. A mai korszerű távcsövek segítségével válaszokat keresünk
a világegyetem létrejöttének módjára, idejére, helyére.
Tekinthetjük őket akár időgépeknek is, hiszen a vizsgált csillagoknak a múltjáról
alkotnak képet, például az egymilliárd fényévnyi távolságra levő csillagnak
egymilliárd évvel ezelőtti állapotát tükrözi. A lencsés távcsöveket színi hibájuk
miatt tükrös távcsövekkel helyettesítették, a fémtükrök korróziója miatt, viszont
még sokáig forgalomban maradtak mindaddig, amíg elkészültek az első ezüstbevonatú
üvegtükrök.
Az 1917-ben Mt. Wilsonon felavatott 100 hüvelyk átmérőjű
tükörrel felszerelt Hooker távcső, „látott”
először a Tejúton túl. A Hooker
távcsővel végzett mérései alapján
közölt első ízben adatokat Edwin
Hubble a szomszédos galaxisok relatív távolságáról
és sebességéről. Hubble legfontosabb eredménye
a világegyetem tágulási sebességének meghatározása.
Hubble 1929-ben felfedezte, hogy a világegyetem minden irányba
állandó sebességgel tágul. A tágulási
sebesség alapján a világegyetem korát tíz
és húsz milliárd év közöttire becsülte.
A Big Bang elmélet ebből a megfigyelésből ered.
A Mt.
Palomar-i Hale tükrös távcső 5 méteres átmérőjű tükrével láthatóvá
váltak a szabad szemmel még észlelhető fényességű csillagoknál 40 milliárdszor
halványabb csillagok is. Hale kimutatta, hogy a tízmilliárd fényévre levő égitestek
között kvázi-csillagok, kvazárok vannak. A kvazárok érdekessége, hogy másodpercenként
kisugárzott energiájuk felér néhány ezer galaxiséval pedig átmérőjük mindössze
milliomod része egy galaxis átmérőjének. A Mt. Palomar
csillagászai hozták először összefüggésbe a kvazárokat a fekete lyukakkal. Segítségével
fedezték fel 2004-ben a Sedna kisbolygót a Naprendszerünkben, pályasugara a
Plutóénak háromszorosa.
A Hubble űrteleszkóp
az első optikai teleszkóp, amelyet 1990-ben Föld körüli pályára állítottak.
Feladatköréül jelölték a Naprendszer tanulmányozását, a világegyetem korának
és méretének a mérését, kozmikus gyökereink keresését, a világegyetem evolúciós
diagramjának elkészítését, valamint a galaxisok, csillagok, bolygók és maga
az élet rejtelmeinek feltárását. A Hubble teljesítményét értékelhetjük azon
fénykép alapján, amelyet 2003-ban készített. A felvétel a világegyetem eddigi
legnagyobb szeletét rögzítette: tízezer galaxist, körülbelül 13 milliárd fényévnyi
kiterjedéssel. Rögzítette csillagok, galaxisok születését, csillagok halálát
(szupernovák). A világegyetem korának a megállapítása úgy történt, hogy a látható
univerzum legtávolabbi, csillaghalálból származó fehér törpéjére fókuszáltak
192 órán keresztül. Erre a hosszú exponálási időre azért volt szükség, mert
annyira halvány, hogy percenként csak néhány foton érkezik róla. A csillagok
távolságát fényességük magnitúdója alapján határozzák meg. E mérés alapján a
világegyetem kora 13.8 milliárd év. A világegyetemről alkotott képünket bonyolítja,
hogy a tágulási sebesség növekszik.
A Keck
ikerteleszkópokat a Hawaii Mauna Kea vulkán tetejére
telepítették. Egyik optikai, a másik infravörös
és 13 milliárd fényévnyi távolságra
„látnak”. Mindkettő méhsejtszerű, harminchat-harminchat
részből álló kisebb külön-külön
számítógép-vezérelt hexagonális tükörből
áll. A fókuszálás pontossága nanométeres
nagyságrendű.
A legérdekfeszítőbb azonban az Arizonában Mt. Graham
hegységben elhelyezett ikerteleszkóp, az LBT (Large
Binocular System). A feladatköre a Földön kívüli életre alkalmas bolygók
felderítése. A Hubble által még jól látott bolygóknál tízszer kisebbekről is
képes éles képet alkotni, úgy hogy kiszűri interferometriás eljárásokkal a csillag
fényét, amely körül keringenek.
Így járul tehát a geometriai fénytan,
a fénytani jelenségek megértésén alapuló
nagyszerű alkalmazások, technikai eszközök révén
az ember jobb életminőségéhez, illetve világképének
kialakulásához.
II. A GEOMETRIAI OPTIKA ALAPJAI
1. ALAPFOGALMAK
Fényforrás az a test, amely fényt sugároz a körülötte
levő térbe. Elsődleges a fényforrás, ha belső energiájának rovására bocsát ki
fényt, illetve másodlagos, ha a ráeső fényt sugározza vissza a térbe. Pontszerű,
ha mérete elhanyagolhatóan kicsi a megfigyelés távolságához képest. Számunkra
a Naprendszeren túli csillagok elsődlegesek és pontszerűnek tekinthetők, míg
Holdunk másodlagos és kiterjedt fényforrásnak.
Fénysugár
A képi gondolkodásunk egyik alapmodellje, amely sok esetben jól leírja a fény
viselkedését, viszont sok esetben nem. Egyaránt használja a fény természetének
leírására a hullám- és a korpuszkuláris elmélet. A korpuszkula elméletben a
korpuszkula (foton) útját, a hullámelméletben a hullámfrontra állított merőlegest
társítják hozzá. A matematikai vonal, félegyenes közelíti leginkább meg. Irányt
és helyzetet jelöl egyszerre, ez a kvantumos viselkedésnek viszont ellentmond.
Pályája homogén közegben egyenes, heterogén közegben görbe. Időbeni szimmetriája
van, azaz a fénymenet megfordítható.
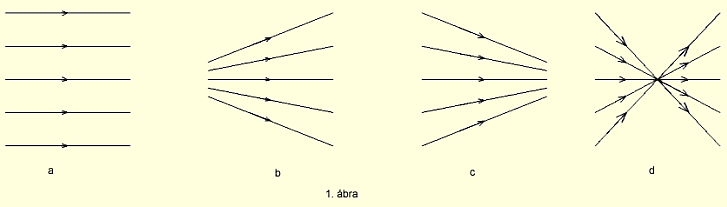
Sugárnyaláb a fénysugarak halmaza. A nyalábot alkotó
sugarak kölcsönös helyzetétől függően megkülönböztetünk párhuzamos, széttartó
vagy divergens, összetartó vagy konvergens, illetve egyközpontú vagy homocentrikus
sugárnyalábot (1. ábra).
Optikai közeg az a térrész, amely nem átlátszatlan
a fény számára. A közegünk lehet anyagi természetű (levegő, víz, üveg...) vagy
vákuum.
Homogén, ha benne nem változik a fény terjedési sebessége.
Törésmutató
Az anyag optikai természetét jellemző mennyiség. Megadja hányszor kisebb az
adott közegben a fény terjedési sebessége, mint vákuumban. Ha a terjedési sebesség
az adott optikai közegben v és vákuumban c, akkor az n törésmutató értéke:
n = c / v (2.1)
Értéke vákuumban 1, a többi optikai közegben
1-nél nagyobb. Homogén anyagban állandó, anizotrop
közegben pontról pontra változhat. A hullámhossztól
is függ, ezért a geometriai optikában monokromatikus fényt
használunk, kivételt képez a diszperzió, mely tárgyalható
a hullámtermészet mélyebb megértése nélkül.
Az optikai rendszerünk geometriai méreteihez képest a fény
hullámhossza, geometriai megközelítésben, elhanyagolhatóan
kicsi kell legyen a hullámjelenségek (diffrakció, interferencia)
kiküszöbölése érdekében.
2. A GEOMETRIAI OPTIKA ALAPELVEI ÉS TÖRVÉNYEI
2.1 A geometriai optika alapelvei
A fény egyenesvonalú terjedésének elve: homogén közegben
egyenes mentén terjed a fény. Következménye, hogy átlátszatlan akadály mögé
nem jut fény. Az akadály mögött létrejövő fényszegény zónát árnyéknak nevezzük.
A fénysugarak függetlenségének elve: a fénysugarak
egymástól függetlenül fejtik ki hatásukat. Keresztezhetik
egymást, nem „ütköznek”.
A sugármenet megfordíthatóságának elve: a fénymenet időszimmetrikusnak
tekinthető. Ugyanazt a fényutat futja be mindkét irányba (akár egy visszafele
lejátszott film). Ha az optikai eszközből kilépett fénysugarat visszatükrözzük,
úgy hogy önmagába verődjön vissza, akkor ugyanazt a fénymenetet figyelhetjük
meg.
2.2 Az eikonál egyenlet
Az eikonálegyenlet a geometriai optika alapegyenlete. Belőle
levezethető a Fermat-elv, következésképpen a geometriai optika alapegyenletei
is.
Az S fényút az A ponttól az M(x,y,z) pontig mérve [9]
az x,y,z koordináták függvénye:
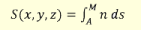 (2.2)
(2.2)
Ezt a vonalmenti integrállal megadott fényutat eikonálnak
is szokták nevezni.
Az S(x,y,z) eikonál a
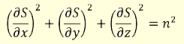 (2.3)
(2.3)
eikonál egyenletnek a megoldása.
Az eikonálegyenlet még felírható
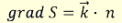 (2.4)
(2.4)
alakban is. A k egységvektor a fénysugár érintőjén van felvéve.
Azokra a pontokra, amelyekre az A pontból kiinduló sugarak fényútja egyenlő,
teljesül az S(x,y,z)=állandó feltétel. Ezek a pontok egy olyan felületet alkotnak,
amely merőleges a k vektorra, tehát magára a fénysugárra. Különböző állandó
értékekre a sugarakra merőleges felületsereget kapunk, ez a következtetés Malus-tételként
ismert.
E tétel szerint bármely egyközpontú nyalábnak bármikor, többszöri törés, visszaverődés
esetében is van normálfelülete [1].
 Az S=állandó és az S+dS=S+n ds=állandó feltételekből:
Az S=állandó és az S+dS=S+n ds=állandó feltételekből:
ds =állandó·1/n
következik, hogy a normálfelületek közötti ds távolság az n törésmutatóval
fordítottan arányos.
Nagyobb törésmutatójú közegekben a normálfelületek távolsága kisebb, ez hatással
van a sugárnyaláb elrendezésére.
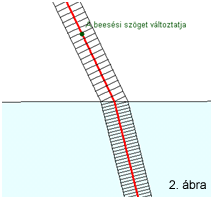
A 2. ábra (KSEG
file letöltése itt) a ritkább optikai közegből érkező hullámfrontok törését
szemlélteti. Megfigyelhető, hogy az alsó optikailag sűrűbb közegben a hullámfrontok
közelebb vannak egymáshoz, mint a felette levő ritkább közegben.
2.3 A Fermat-elv
Két pont között, amelyeken a fénysugár áthalad, az optikai
úthossznak szélsőértéke van. Ha a két pont között más, szomszédos úton haladna
a fénysugár, akkor később jutna el. Homogén közegben a szélsőértéknek az egyenes
felel meg, különböző egymással határos homogén közegekben törtvonal.
Az elv egyaránt érvényes egy optikai rendszer egészére vagy annak tetszőleges
részére, tehát a fénysugár bármely szakaszára. Egy pont képének létrejöttéhez
a pontról kiinduló több kissé különböző fényutat befutó sugárnak kell újból
találkozni. A leképezés sztigmatikusnak tekintett, amennyiben a szomszédos útvonalak
egy olyan kontinuumot alkotnak melyek hossza egyenlő. Amennyiben közeliek, de
kissé eltérő hosszúak, akkor az egyenlőségtől való eltérés lesz a képi aberráció
mértéke.
Ezen elv segítségével levezethetőek a fényvisszaverődés és fénytörés törvényei.
A természet takarékos módon bánik a változással kapcsolatos jelenségek esetében.
Ezt erősíti meg Fermat fényterjedésre vonatkozó elve.
Heterogén optikai közegben a törésmutató pontról pontra változhat, így a töréstörvény
már nem alkalmazható.
A (2.2) összefüggés szerint a fénysugár az A ponttól a B pontig
(3. ábra) az
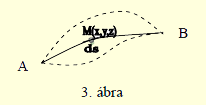
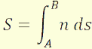
integrállal kifejezhető fényutat teszi meg.
Az M(x,y,z) futópont környezetében a törésmutató n=n(x,y,z)függvénnyel jellemezhető.
A ds ívelem a fényútnak infinitezimális szakasza az M pont környezetében. A
Fermat-elv szerint a fénysugár mentén a fényút variációja [9] nulla:
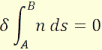 (2.5)
(2.5)
A Fermat-elv határesetként tartalmazza a fényvisszaverődés
és fénytörés törvényét.
Homogén optikai közegben a törésmutató állandó, kikerül az integrál alól. Az
integrál ez esetben a geometriai utat jelenti. A fényútnak akkor van szélsőértéke,
amikor a geometriai úthossznak, azaz:
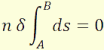
Homogén közegben két pont között a legrövidebb geometriai
út az őket összekötő egyenes szakasz, tehát a fény egyenes mentén terjed benne.
2.3.1 A fényvisszaverődés
 Fényvisszaverődésnek nevezzük azt a fényjelenséget mikor két
optikai közeget elválasztó határfelületre eső fény visszatér abba a közegbe,
ahonnan érkezett.
Fényvisszaverődésnek nevezzük azt a fényjelenséget mikor két
optikai közeget elválasztó határfelületre eső fény visszatér abba a közegbe,
ahonnan érkezett.
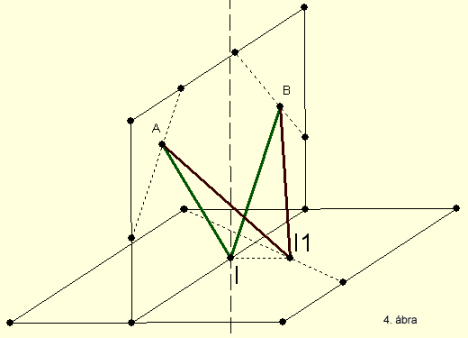
A 4. ábra két egymásra merőleges síkot
mutat.
A vízszintes sík jelenti a két közeget elválasztó határfelületet. A határfelületre
merőleges, függőleges síkban van két pont: A és B. Feltételezzük, hogy a fénysugár
A-ból a határfelületre, majd innen B-be jut. Felveszünk a határfelület síkjában
egy tetszőleges I1 pontot. I1-nek a függőleges síkra eső vetülete az I pont.
A szerkesztésből adódik, hogy I1IA és BII1 derékszögek.
Mivel AI1(átfogó)>AI(befogó) és BI1(átfogó)>BI(befogó) az AI1+I1B fényút
hosszabb az AI+IB fényútnál, ennélfogva az AI-beeső-, az IB-visszavert sugarak
és az IN beesési merőleges egy síkban vannak. Ez a fényvisszaverődés egyik törvénye.
Annak a megállapítására, hogy az I pont hol helyezkedik el a két sík metszésvonalán,
a mellékelt 5. ábrán látható szerkesztésből
indulunk ki.
 A síktükör az A pontból feléje tartó sugarat a B ponton keresztül
veri vissza. Feltételezzük, hogy a fénysugár az I pontból verődik vissza. Meghatározzuk
az I beesési pont helyzetét úgy, hogy az AIB utat a fény a legrövidebb idő alatt
tegye meg. Ehhez meghatározzuk y értékét. Adottnak tekinthetők a h1, h2 tükörig
mért távolságok, valamint az A és B pontok tükörre eső vetületeinek a w távolsága.
A síktükör az A pontból feléje tartó sugarat a B ponton keresztül
veri vissza. Feltételezzük, hogy a fénysugár az I pontból verődik vissza. Meghatározzuk
az I beesési pont helyzetét úgy, hogy az AIB utat a fény a legrövidebb idő alatt
tegye meg. Ehhez meghatározzuk y értékét. Adottnak tekinthetők a h1, h2 tükörig
mért távolságok, valamint az A és B pontok tükörre eső vetületeinek a w távolsága.
Az I pontban a tükörre állított beesési merőlegessel a beeső fénysugár i
beesési szöget, míg a visszavert fénysugár r
visszaverődési szöget zár be.
Az AIB út megtételéhez szükséges idő:
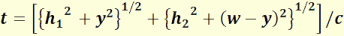 (2.6)
(2.6)
Differenciálva t-t az y változó szerint, az alábbi összefüggést
kapjuk:
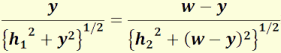 (2.7)
(2.7)
Észrevehető, hogy az egyenlet bal oldala sin(i),
jobboldala pedig sin(r). Innen adódik, hogy az i
beesési szög egyenlő az r visszaverődési szöggel.
i = - r
(2.8)
A 2.8-as összefüggésben a negatív előjel azt mutatja, hogy
a beesési merőlegestől a visszavert sugárig az óramutató járásával megegyező
irányban mérjük a visszaverődési szöget.
Ez a szögekre levezetett összefüggés kiegészítve azzal, hogy a beeső fénysugár,
a beesési merőleges és a visszavert fénysugár egy síkban van, jelentik a fényvisszaverődés
törvényeit. Megjegyzendő, hogy az A és B pontok közötti terjedési időnek lokális
és nem globális minimuma van, ugyanis A-ból B-be a tükör érintése nélkül megtett
út, az AB-szakasz mentén a legrövidebb.
2.3.2 A fénytörés
Fénytörés akkor lép fel, ha két eltérő törésmutatójú, homogén
optikai közeg határfelületére érkező fény terjedési iránya megváltozik, miközben
áthatol a másik optikai közegbe. A határfelületre érkező fénysugarat beeső-,
a másik közegbe behatoló sugarat megtört fénysugárnak nevezzük. A beesési pontban
a határfelületre állított képzeletbeli egyenes a beesési egyenes.
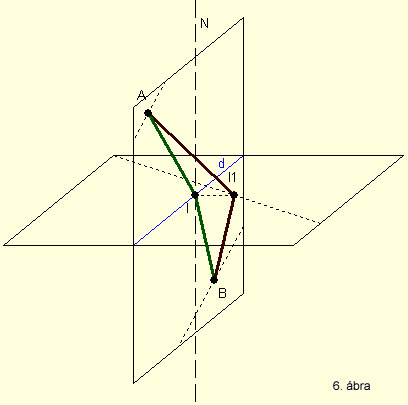 Annak az igazolására, hogy a beesési merőleges, a beeső- és a visszavert fénysugár
egy síkban van, tekintsük a 6. ábrát.
(KSEG file letöltése itt)
Annak az igazolására, hogy a beesési merőleges, a beeső- és a visszavert fénysugár
egy síkban van, tekintsük a 6. ábrát.
(KSEG file letöltése itt)
A vízszintes sík a határfelületet jelenti, a határfelületre
merőleges síkban vannak az A és B pontok. Az A pontból kiinduló fénysugár a
B pontba érkezik. Feltételezzük, hogy a fény a határfelület tetszőleges I1 pontján
keresztül halad át. A Fermat-elv alapján az AI1B fényútnak minimuma van. AII1
és I1BI derékszögű háromszögekben AI1 és BI1 átfogók, tehát AI1>AI és I1B>IB,
következésképpen AI1+I1B>AI+IB, ennélfogva az AIB útvonal rövidebb. I viszont
a két sík metszeti egyenesén van, tehát igazoltuk, hogy a beesési merőleges
(IN), a beeső- és a megtört fénysugár egy síkban vannak.
Annak kiderítésére, hogy a két sík metszésvonalán hol helyezkedik el az I beesési
pont, tekintsük a 7. ábrát.
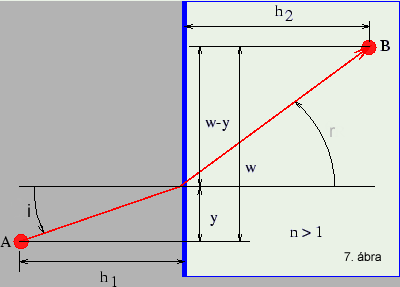 A
szürkével jelölt sűrűbb optikai közeg A pontjából a jobboldali, ritkább optikai
közeg B pontjába érkezik a fénysugár. Tudva, hogy a közegek homogének és bennük
egyenes mentén terjed a fény, a feladat az I beesési pont helyzetének a meghatározására
korlátozódik, ezt az y változóval jellemezzük. A vákuumban való terjedéshez
képest a két közegben a terjedési idő n1 illetve n2-ször
nagyobb.
A
szürkével jelölt sűrűbb optikai közeg A pontjából a jobboldali, ritkább optikai
közeg B pontjába érkezik a fénysugár. Tudva, hogy a közegek homogének és bennük
egyenes mentén terjed a fény, a feladat az I beesési pont helyzetének a meghatározására
korlátozódik, ezt az y változóval jellemezzük. A vákuumban való terjedéshez
képest a két közegben a terjedési idő n1 illetve n2-ször
nagyobb.
A terjedési sebességek v1=c / n1 és v2=c /
n2.
Az út időtartama pedig:
 (2.9)
(2.9)
Differenciálva az időt y szerint, majd a kapott
összefüggést zéróval egyenlővé téve és megoldva kapjuk:
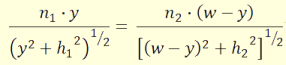 (2.10)
(2.10)
n1 ·sin i
= n2 · sin r
(2.11)
Ez pedig a Snellius—Descartes
összefüggés a homogén közegpárok határfelületén
bekövetkező fénytörés jelenségére.
Az összefüggésből kiderül, hogy a nagyobb törésmutatóhoz kisebb szög tartozik,
ami intuitíven azt jelenti, hogy a fénysugár a sűrűbb közegbe érve lelassul
és a beesési merőlegeshez közeledik.
Abból, hogy a beesési szög értéke [0,90] közötti lehet csak, néhány sajátos
eset adódik:
Legyen például a beesési szög i = 0. Mivel a törésmutató zérus nem
lehet, következik, hogy a törési szög is zéró, tehát nincs fénytörés.
2.3.3 A teljes fényvisszaverődés
Határszögnek nevezzük és L-lel jelöljük azt
a beesési szöget, amelyre a törési szög r = 90°. Mivel ritkább közeghez
nagyobb szög tartozik, ebből arra következtetünk, hogy ez esetben a fény sűrűbb
közegből érkezik ritkábba. A 2.11-es összefüggésből
L = arcsin(n2
/ n1)
(2.12)
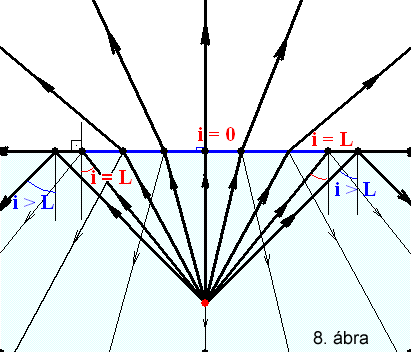 Mivel a szögek egyaránt nőnek vagy csökkennek (de nem arányosan),
emiatt i > L –re nincs valós megoldás, mert r
nem lehet 90 foknál nagyobb. Valóban L-nél
nagyobb értékekre nincs fénytörés, a fellépő jelenség a teljes fényvisszaverődés.
A jelenség szemléltetése a 8. ábrán (KSEG
file letöltése itt) figyelhető meg. Látható, hogy merőleges beeséskor a
fény belép ugyan a ritkább közegbe, de terjedési iránya változatlan marad. Határszögnél
nagyobb értékekre a határfelület tökéletes tükörként viselkedik. Fénytörés tehát
akkor van, ha a törésmutatók különböznek és i <= L, míg
teljes visszaverődés L<i<90 fok esetén.
Mivel a szögek egyaránt nőnek vagy csökkennek (de nem arányosan),
emiatt i > L –re nincs valós megoldás, mert r
nem lehet 90 foknál nagyobb. Valóban L-nél
nagyobb értékekre nincs fénytörés, a fellépő jelenség a teljes fényvisszaverődés.
A jelenség szemléltetése a 8. ábrán (KSEG
file letöltése itt) figyelhető meg. Látható, hogy merőleges beeséskor a
fény belép ugyan a ritkább közegbe, de terjedési iránya változatlan marad. Határszögnél
nagyobb értékekre a határfelület tökéletes tükörként viselkedik. Fénytörés tehát
akkor van, ha a törésmutatók különböznek és i <= L, míg
teljes visszaverődés L<i<90 fok esetén.
A jelenségnek óriási a jelentősége, mert lehetővé teszi a fényenergia veszteségmentes
szállítását az optikai szálon keresztül. Ennek keresztmetszete kör
és közepétől sugárirányban távolodva optikailag egyre ritkább, emiatt a fény
belőle gyakorlatilag nem tud kilépni csak a szál végén. Ez lehetővé teszi az
információ akár több kilométeres, veszteségmentes továbbítását. Alkalmazási
területe széles, az endoszkóptól, a telefonos, internetes, kábeltelevíziós hálózatokig
terjed.
2.3.4 A diszperzió
A színszóródást nevezik diszperziónak. A jelenség azon alapszik,
hogy ugyanabban az optikai közegben a különböző színű fénysugarak terjedési
sebessége is különböző. A színek jellemzésére használható a frekvencia, illetve
a hullámhossz. A látható fény spektruma a vöröstől az ibolyaszínig tart. A vörös
hullámhossza a legnagyobb, az ibolyaszíné a legkisebb.
A λ hullámhossz kifejezhető a vákuumban mért
c fénysebesség és a ν frekvencia segítségével:
λ
= c / ν
(2.13)
E = h·ν
(2.14)
A fény korpuszkuláris elmélete alapján egy fényrészecske, foton az elektromágneses
hullám legkisebb energiacsomagja:
Vonal |
Elem |
Hullámhossz (nm) |
Szín |
A |
kálium |
768,22 |
vörös |
C |
hidrogén |
656,28 |
vörös |
D |
nátrium |
589,3(kettős vonal)
|
sárga |
d |
hélium |
587,6 |
sárga |
F |
hidrogén |
486,13 |
kék |
G |
hidrogén |
434,05 |
indigó |
h = 6.626068 × 10E-34 J.s, a Planck-állandó.
A kvantumelméletben az impulzusnyomatékot kvantálja, az energia eloszlásának
diszkrét értékeire utal, egyike a legkisebb fizikai állandóknak. A (2.14) értelmében
a látható fény tartományában a vörös fényhez tartozik a legkisebb és az ibolyához
a legnagyobb energia.
Mivel a törésmutató n = n(λ), ez a különböző színek
szétválásához vezet fénytörés esetén. Víz esetében például a vörös fényre 1.332,
míg ibolyára 1.343 a törésmutató értéke [6]. A diszperziót a különböző monokromatikus
sugarakra megállapított törésmutató értékekkel jellemzik. Ezek a sugarak különböző
kémiai elemek színképvonalainak felelnek meg.
A fenti táblázat néhány kémiai elem színképvonalának hullámhosszát tartalmazza:
Közepes diszperziónak nevezik a Δn = nF - nC
értéket, Abbe-számnak
a ν = (nd - 1) / (nF - nC)
arányt.
Hartmann empirikus
diszperzió függvénye:
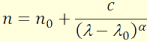 (2.15)
(2.15)
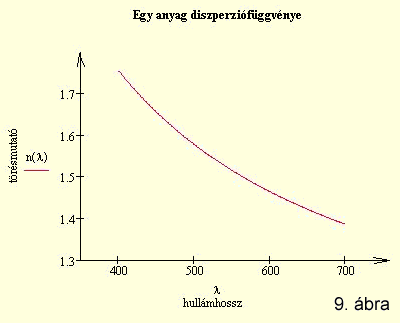 Az n0, c, λ0 és α0 empirikus állandókat
négy hullámhosszra megmért törésmutató értékekből határozzák meg [9]. α
értéke körülbelül 1.2, de 1-re is elég pontos
a közelítés és elegendő három hullámhosszra
elvégezni a méréseket. A 9. ábra
egy anyag diszperzió függvényét szemlélteti
a 400 – 700 nm-es tartományban.
Az n0, c, λ0 és α0 empirikus állandókat
négy hullámhosszra megmért törésmutató értékekből határozzák meg [9]. α
értéke körülbelül 1.2, de 1-re is elég pontos
a közelítés és elegendő három hullámhosszra
elvégezni a méréseket. A 9. ábra
egy anyag diszperzió függvényét szemlélteti
a 400 – 700 nm-es tartományban.
A diszperzió jelensége eredményezi a szivárvány létrejöttét. Az esőcseppen áthaladó
fehér fény két fénytörés és egy visszaverődés eredményeként bomlik a szivárvány
színeire.
2.3.5 Refraktometria
Az anyagok törésmutatójának meghatározásával foglalkozik. Refraktométer-
olyan berendezés, amely a teljes visszaverődés határszög mérését teszi lehetővé.
Ebből meghatározható a relatív törésmutató.

A 10. ábrán (KSEG
file letöltése itt) egy Pulfrich refraktométer van szemléltetve. A felső
anyag törésmutatója meghatározható az alsó törésmutató és az i2 szög
ismeretében. Alapfeltétel, hogy kisebb törésmutatójú legyen az ismert anyagénál
és a párhuzamostól alig eltérő monokromatikus nyaláb mintegy csak súrolja a
két test határfelületét. Ekkor a nyaláb teljes egészében az alsó térrészbe jut.
Addig forgatjuk a távcsövet, amíg látómezejének csak fele lesz megvilágított.
E módszerrel 10-4, 10-5 nagyságrendű pontossággal határozható
meg a törésmutató.
A színképelemzés vagy spektroszkópia a diszperzió jelenségén alapszik. Számunkra
a csillagok sugárzással fedik fel tulajdonságaikat, kémiai összetételüket. A
színképelemzés azon alapszik, hogy az atomok diszkrét energia szintjeiknek megfelelő
sugárzást bocsátanak ki (színképvonalai úgy azonosítják
az atomot, mint embert a DNS-e), amelyek csak az adott atomra jellemzőek. Ha
tehát fehér fénnyel megvilágítjuk őket, az elnyelés csak az energiaszinteknek
megfelelő lehet, az abszorpciós színképből hiányoznak az elnyelt hullámhosszúságú
sugarak, ha pedig gerjesztjük őket, akkor az elektronátmeneteknek megfelelő
hullámhosszú sugárzást bocsátanak ki. Ezeket egy fénytani prizmán átbocsátva
különválasztjuk és táblázati értékekkel egybevetve megállapítjuk a kibocsátó
kémiai elem típusát.
3. OPTIKAI KÉPALKOTÁS
3.1 A képalkotás fogalmai
Képalkotáson egy tárgy képének optikai eszközökkel való létrehozását
értjük. A tárgy egy pontját pontszerű fényforrásnak tekintjük. A róla kiinduló
sugarak egy része szűk homocentrikus nyalábban az optikai eszközön áthaladva,
a különböző fényjelenségek eredményeként irányt változtatva megy át. Az optikai
eszközt elhagyó sugarak metszéspontjában keletkezik a tárgypont képe. Leképzés:
a tárgypontok és képpontok közötti függvénykapcsolattal leírható megfeleltetés.
Az összetartozó tárgy és képpontokat egymás “konjugáltjainak” nevezzük.
Nyaláb fókuszpontja olyan pont, ahol az azonos tárgypontból érkező, szomszédos
sugarak a képtérben elsőrendben egy pontban metszik egymást.
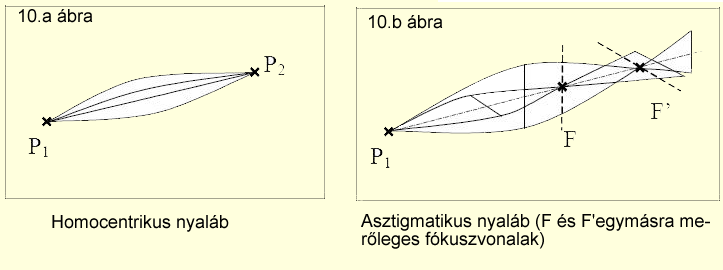
Amennyiben az optikai eszközt elhagyó nyaláb is egyközpontú, akkor a leképezés
pontszerű vagy sztigmatikus (10.a ábra).
Asztigmatikus leképezéskor nincs egyértelmű megfeleltetés tárgypont és képe
között, ilyenkor egy tárgypontnak több képpont felel meg. Ezek a képpontok két
egymásra merőleges fókuszvonalon helyezkednek el (10.b
ábra).
A kép valódi amennyiben a sugarak ténylegesen metszik egymást, ekkor az eszköz
mögött alkalmasan elhelyezett ernyőn felfogható a kép. Ha a kilépő nyaláb széttartó,
akkor sugarainak visszafele való képzeletbeli meghosszabbításának metszéspontjában
látszólagos (virtuális) kép keletkezik. A szemünk a fénysugarak szögviszonyainak
megfelelően alkot képet, ezért úgy tűnik mintha ebből a pontból indult volna
ki a nyaláb.
Széttartó nyalábnak mindig valódi tárgypont feleltethető meg, még akkor is,
ha a széttartó nyaláb egy másik optikai rendszer látszólagos képpontjából eredt.
Az optikai eszköz számára a ráeső összetartó sugárnyaláb látszólagos tárgyat
eredményez.
Paraxiális nyaláb esetében a fénysugarak forgástengelytől mért távolsága, illetve
a tengellyel bezárt szöge is zéróhoz tart. Az elsőrendű közelítés azt a matematikai
approximációt jelenti, hogy a helyzetek és irányok matematikai feldolgozása
az első nagyságrendig van figyelembe véve szögek és vonalas méreteket illetően.
Például a szinusz-függvény sorba fejtésének csak az első tagját vesszük figyelembe:
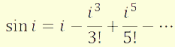
tehát paraxiális sugárra sin i = i. [10] Amennyiben
a paraxiális feltétel nem teljesül, a következő tagot is figyelembe vesszük,
ami harmadrendű megközelítést jelent ez esetben, a második tag hatványkitevő
értékének megfelelően.
Egy kiterjedt tárgy felületét alkotó tárgypontoknak megfeleltetett képpontokból
áll a tárgy képe.
Abszolút műszer: olyan optikai rendszer, amely egy tartomány minden pontját
sztigmatikusan, konstans nagyítással képezi le.
Aplanatikus leképzés: P2 pont akkor aplanatikus képe P1-nek,
ha P1 elsőrendűen kicsi körlap alakú környezetének pontjai P1-el
együtt szintén sztigmatikusan képződnek le. Ekkor P1 és P2-t aplanatikus
pontpárnak nevezik.
Meridionális sík: forgásszimmetrikus rendszerben a tengelyt magában foglaló
tetszőleges sík.
Tárgytér és képtér a tárgypontok illetve képpontok végtelen kiterjedésű tere.
Mindkettő lehet valódi vagy virtuális, aszerint hogy fizikailag hozzáférhetőek
vagy sem. A fizikai térrel, optikai közeggel nem tévesztendők össze. Fedésbe
is lehetnek egymással fényvisszaverő optikai eszközök esetében. A tárgytéri
mennyiségeket 1-es, a képtérieket 2-es indexszel jelöljük.
A lineáris (transzverzális) vagy vonalas nagyítás a kép és a tárgy lineáris
méretének aránya:
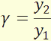 (3.1)
(3.1)
A kép kicsinyített, ha |γ|<1 és nagyított |γ|>1 esetében.
Értéke bármekkora lehet - ∞ és+∞ között. A pozitív érték egyenes-,
a negatív fordított állású képet jelent.
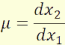 (3.2)
(3.2)
A mélységi vagy longitudinális nagyítás, a tárgy forgástengely
mentén vett kis dx1 tárgy- és dx2 képméretek segítségével
értelmezett.
A szögnagyítást látszólagos kép esetén célszerű értelmezni. Az optikai eszköz
alkotta kép méretével arányosan kicsinyített kép keletkezik a retinánkon (11.
ábra).
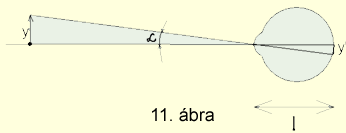
y’= l·tgα a szemünkben keletkező kép lineáris
mérete tgα–val arányos mivel l gyakorlatilag állandó.
Ha α2 szög alatt látjuk a tárgy optikai eszköz
által alkotott képét, és α1 alatt a tárgyat
szabad szemmel, akkor y2 = l·tgα2 és
y1 = l·tg α1 Innen:
y2/y1≈ tgα2/ tg α1
Amennyiben a tárgy helyzetének változtatása lehetséges, a tárgyat a minimális
tisztánlátási távolságba (25 cm) helyezve határozzuk meg a tg α1 értékét.
Az optikai eszköz G szögnagyítását a
G = tg α2/tg α1
(3.2')
kifejezés adja.
Tökéletes képalkotás akkor van, ha a leképezés sztigmatikus, aplanatikus és
a lineáris nagyítás a tárgy bármely részére állandó. Ezek a feltételek maradéktalanul
kevés esetben teljesülnek, ilyenkor képi hibák jelennek meg.
3.2 Gauss optika
A geometriai optikának olyan megközelítése, amelyben
tökéletes képalkotást feltételezünk. Ilyen idealizált esetekben nem lépnek fel
képi hibák, a matematikai leírásmód egyszerű. A jelenségek könnyen szemléltethetők
és tárgyalhatok. A líceumi tankönyvekben a geometriai fénytan jelenségeit Gauss
féle megközelítésben tárgyalja.
Feltevések:
- a tárgy és képtér homogén
- az optikai műszer forgásszimmetrikus az optikai tengelyre nézve
- elsőrendű közelítés (paraxiális sugarak)
- található legalább egy sugár, amely a tengelyt a tárgy- és képtérben
is metszi
Következmény: paraxiális közelítésben az optikai rendszer az
egész tárgyteret sztigmatikusan képezi le. Ez azt jelenti, hogy a tárgytér és
képtér pontjai egymásnak konjugáltjai.
3.3 Centrált rendszerek
Értelmezés szerint olyan optikai rendszerek,
amelyek tengelyszimmetrikus leképezést nyújtanak. Az optikai
eszköz szimmetriatengelyét optikai tengelynek nevezzük. Az
optikai tengely pontjainak képe is az optikai tengelyen van. A tengelyre
merőleges tárgy-síknak megfelelő konjugált
kép-sík is merőleges az optikai tengelyre.
A kardinális elemek olyan pontok, egyenesek és síkok halmaza, amelynek kitüntetett
szerepe van a leképezésben. (12. ábra)
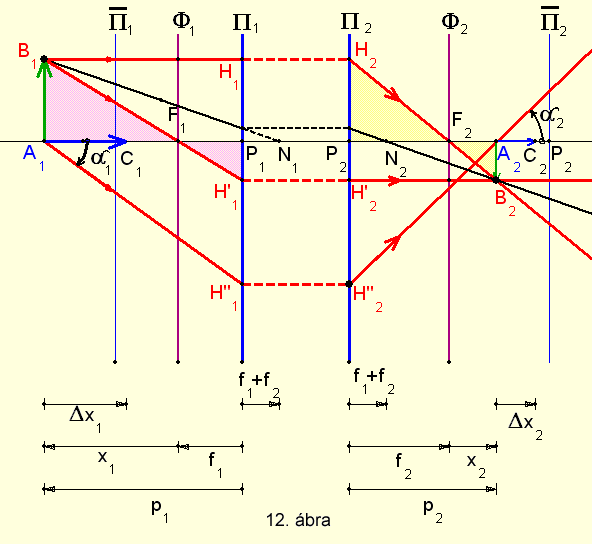
(KSEG file letöltése itt)
Képoldali fókuszpont, F2 az optikai tengellyel a centrált rendszerre
párhuzamosan eső sugarak e pontban metszik egymást miután elhagyták az optikai
rendszert.
Tárgytérbeli fókuszpont, F1 az optikai tengely azon pontja, amelynek
konjugáltja a képtéri végtelenben van.
Tárgytéri fókuszsík, a tárgytéri fókuszpontban az optikai tengelyre merőleges
sík Φ 1.
Képtéri fókuszsík, a képtéri fókuszpontban az optikai tengelyre merőleges sík
Φ 2 .
Fősíkok a γ = +1 vonalas nagyításnak megfelelő konjugált
síkpár Π1, Π2.
Főpontok P1, P2 a fősíkok és az optikai tengely metszéspontjai.
f1 = P1F1, f2 = P2F2 tárgytérbeli-,
képtérbeli fókusztávolságok.
A következő jelölések lettek bevezetve: A1B1 = y1
és A2B2 = y2 transzverzális tárgy és kép méret.
F1A1 = x1, F2A2=x2
a fókuszsíkoktól mért tárgy és képtávolság. P1A1 = p1
és P2A2 = p2 a fősíkoktól mért tárgy és képtávolság,
N1 és N2 csomópontok.
A 12. ábrán a lila kitöltésű és sárga kitöltésű
háromszögek hasonlóságából a vonalas nagyításra:
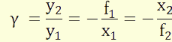 (3.3)
(3.3)
és ebből az
x1·x2 = f1·f2
(3.4)
Newton képlet
adódik.
Ha referenciának a fősíkoktól mért távolságokat vesszük, akkor az x1
= p1 - f1 és x2 = p2
- f2 távolságokat a (3.4)-be helyettesítve, a képalkotási
egyenletet kapjuk:
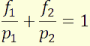 (3.5)
(3.5)
A szögnagyítás:
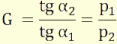 (3.6)
(3.6)
Az A1 pontból az optikai tengellyel α1
szöget bezáró kiinduló sugár az A2
konjugált pontba az optikai tengellyel α2 szöget
bezárva jut. A G szögnagyításra az A1P1H1"
és A2P2H2" derékszögű
háromszögekben felírt szögek tangenseinek arányából:
ami kifejezhető a x1, x2, valamint f1 és f2
ismeretében a
G = x1
/ f2 =f1 / x2
(3.7)
összefüggésekkel.
Az optikai tengelyen fekvő A1C1 tárgyról A2C2
méretű képet alkot az eszköz, a mélységbeli vonalas nagyítása a Newton-képlet
differenciált alakjából számítható.
Δx1·x2+x1·Δx2 = 0 és ebből
µ = Δx2
/ Δx1 = - x2 / x1
(3.8)
A fősíkoktól mért távolságokkal pedig
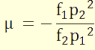 (3.9)
(3.9)
képlettel számítható.
A három nagyítás közötti összefüggésünk:
γ = G·µ
(3.10)
A vonalas nagyítás a fősíkoktól mért távolságokkal:
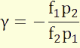 (3.11)
(3.11)
A csomópontoknak a megfelelő főpontoktól mért távolsága P1N1
és P2N2 és mivel egymásnak konjugáltjai a képalkotási
egyenletbe helyettesítve, valamint a (3.6) alapján:
P1N1
= P2N2 = f1 + f2
(3.12)
Az eredményeket összefoglalva megállapítható, hogy a centrált rendszer képalkotás
tekintetében egyértelműen meghatározott, ha ismert két konjugált síkpárjának
a helyzete vagy egy síkpárjának és két fókuszpontjának helyzete.
3.4 Centrált rendszerek egyesítése
Ismert adatú optikai rendszerek egyesítésével új optikai rendszert
kapunk. Az első optikai rendszer képtere a második rendszer tárgyterét képezi.
Ezt képezi le a második rendszer az egyesített rendszer képterébe. A részrendszerek
kardinális elemeinek ismeretében meghatározhatók az egyesített rendszer kardinális
elemei.
Optikai köznek vagy tubushossznak nevezzük a részrendszerek egymáshoz viszonyított
távolságát. Ezt a második rendszer tárgytéri- és az első rendszer képtéri fókuszpontjai
között mérjük:
Δ = F1´´F2´
(3.13)

A 13. ábra alapján (KSEG
file letöltése itt) meghatározhatók az egyesített rendszer kardinális adatai.
Az alábbi jelöléseket vezettük be: 1 tárgytérre, 2 képtérre vonatkozó adatok,
´ az első-, ´´ a második rendszerre vonatkozik. φ1, φ2
az egyesített rendszer fókuszsíkjainak távolsága az első rendszer tárgytéri-,
illetve a második rendszer képtéri fősíkjáig, d1 = P1´P1,
d2 = P2´´P2 az egyesített rendszer fősíkjainak
a helyzete az első rendszer tárgytéri fősíkjához valamint a második rendszer
képtéri fősíkjához képest.
Az optikai tengellyel párhuzamosan h magasságban belépő sugár végül F2-ben
metszi az optikai tengelyt. Ahhoz, hogy meghatározhassuk F2 helyét
segédszerkesztést végzünk. Az F2´-en áthaladó sugár és a második
rendszer tárgyéri fókuszsíkjának metszeti pontjából az optikai tengellyel párhuzamos
sugarat húzunk, ez a sugár a második rendszer képtéri fókuszán megy át. Mivel
a fókuszsík egy pontjából kiinduló sugarak a rendszer túlsó oldalán párhuzamosak,
ezért vele párhuzamos lesz a rendszert elhagyó sugár. Fordított sugármenettel
analóg módon határozzuk meg F1 helyzetét.
A második rendszerre vonatkoztatva F2 és F2´ egymásnak
konjugáltjai és Δ valamint F2´´F2 szakaszokra felírható
Newton-képletből:
Δ·F2´´F2
= f1´´·f2´´
meghatározható a φ2 gyújtósík helyzete.
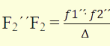 (3.14)
(3.14)
A második rendszer szögnagyítása az α1 alatt
belépő és α2 szög alatt kilépő sugárra

ahonnan
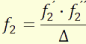 (3.15)
(3.15)
A fénymenet megfordíthatóságának elvéből az 1↔2, ´↔´´
és a Δ ↔-Δ transzformációkkal megkapható a tárgytéri fókuszsík
helyzete is:
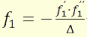 (3.16)
(3.16)
Nagy gyakorlati jelentősége van a φ1,φ2,
d1, d2 távolságok ismeretének.
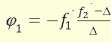 (3.17)
(3.17)
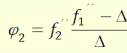 (3.18)
(3.18)
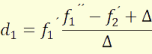 (3.19)
(3.19)
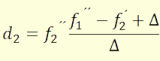 (3.20)
(3.20)
Az egyesített rendszer nagyításai a részrendszerek nagyítóképességeinek szorzataként
adhatók meg:
µ = µ´·
µ´´, γ = γ´·γ´´,
G = G´·G´´ (3.21)
Afokális vagy teleszkopikus optikai rendszernek a Δ =
0 tubushosszúságú rendszert nevezzük. Az ilyen rendszernek végtelenben vannak
a fókuszpontjai, tehát párhuzamos nyalábot párhuzamos nyalábba képez le (14.
ábra). (KSEG file letöltése
itt)
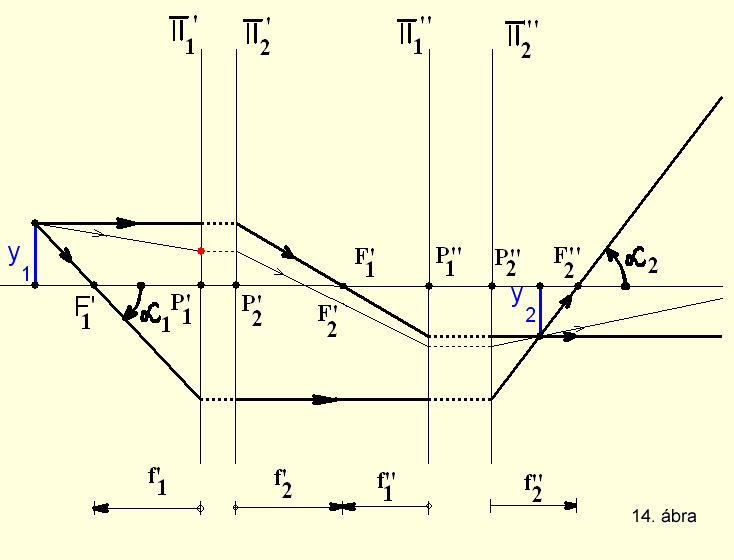
Teleszkopikus mert a teleszkópokra jellemző ez a sajátosság.
Állandó nagyításokkal dolgozik, a tárgy helyzetétől
függetlenül.
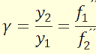 (3.22)
(3.22)
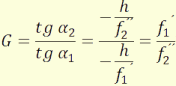 (3.23)
(3.23)
 (3.24)
(3.24)
A fenti egyenleteket úgy kaptuk, hogy behelyettesítettük a
(3.21)-be a részrendszerek nagyításaira kapott összefüggéseket.
4. OPTIKAI RENDSZEREK
A fejezetben különböző optikai rendszerek képalkotási sajátosságai
kerülnek bemutatásra.
4.1 Gömb törőfelület
Két egymással egy gömbfelszín (gömbsüveg) mentén határos homogén
törésmutatójú optikai közegpárból álló egyszerű optikai rendszer. A két közeg
törésmutatója n1 és n2 értékű. R a gömbfelszín sugara,
V a tetőpont, A1 tárgypont és adott i beesési szög mellett a neki megfelelő
A2 képpont (15. ábra).
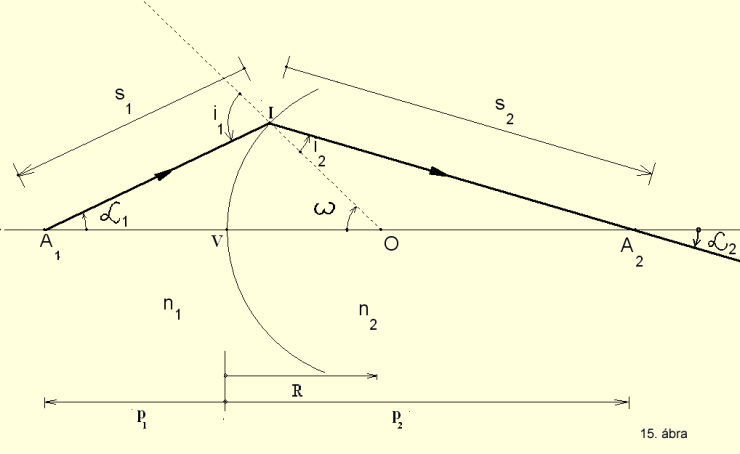
(KSEG file
letöltése itt). A gömbfelszín forgási szimmetriája miatt végtelen számú optikai
tengely értelmezhető, emiatt a tárgypontot a felszín görbületi középpontjával
összekötő képzeletbeli egyenest optikai főtengelynek nevezzük és hozzá képest
adunk meg szög és távolság adatokat.
Az optikai főtengellyel α1 szög alatt érkező sugár a törőfelületet
az I beesési pontban metszi és i1 szöget zár be az I-re állított
beesési merőlegessel. A törési szöget i2 jelöli. ω a beesési
merőleges főtengellyel bezárt szöge. A megtört sugár a főtengellyel α2
szöget zár be. A p1 = VA1 és p2 = VA2
a tárgy- és képpont tetőponttól mért távolsága. s1 = IA1
és s2 = IA2 a beesési ponttól mért szagittális tárgy-
és képtávolság.
Előjelszabály: jobbról balra mutató távolságok és az óramutató járási irányában
mért szögek negatívak.
A 15. ábra alapján a háromszögek területei
között fennálló
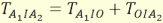 (4.1)
(4.1)
összefüggésből és az általános
ABC háromszög területképletéből (TABC
= a·b·sinC/2) valamint a szakaszok és szögek
előjeles behelyettesítéséből adódik
a gömb törőfelület szagittális képalkotási
egyenlete:
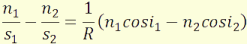 (4.2)
(4.2)
Az egyenlet és a forgásszimmetria alapján belátható, hogy az
A1-ből i1 szög alatt beeső sugarak egy 2α1
nyílásszögű s1 hosszú alkotótójú és A1 csúcsú kúpfelszínt
képeznek és egy A2 csúcsú 2α2 nyílásszögű, s2
alkotójú kúpfelszínbe képződnek le.
A leképezés nem sztigmatikus, A1-nek megfelelő szagittális képpontok
a főtengely mentén a beesési szög függvényében helyezkednek el (16.
ábra).
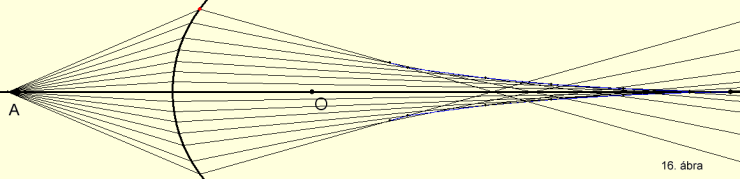
A baloldali tárgypont képe a megtört szomszédos sugarak metszéspontjaiból
álló forgásfelszín lesz. A 16. ábrán (KSEG
file letöltése itt) kék színnel lett ez a felület megjelölve. Ezt a felületet
nevezzük tangenciális képnek.
A tangenciális képalkotás egyenletéhez tartozó mennyiségek a 17.
ábrán szemlélhetők meg.
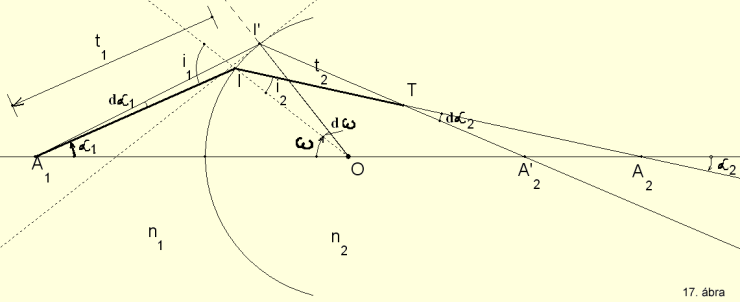
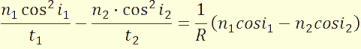 (4.3)
(4.3)
ahol t1 = A1I, t2 = IT a tangenciális tárgy-
és képtávolság. Az A1 pontból dα1 elemi nyílásszögű
nyaláb indul ki és törés után a T pontban képezi le A1-et.
A szagittális képszakasz és a tangenciális képfelület a beeső nyaláb 2α1
nyílásszögének csökkentésével érhető el. Ha a nyaláb nyílásszögét nagyon picire
csökkentjük, akkor már a paraxiális nyaláb jó képet ad.
Gauss féle megközelítésben i1≈0, valamint s1 = t1
= p1 és s2 = t2 = p2 a képalkotási
egyenletek az alábbi formára egyszerűsödnek:
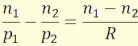 (4.4)
(4.4)
Ebben az esetben a képtávolság csak a törésmutatóktól, a görbületi sugártól
és a tárgytávolságtól függ.
p1 = ∞-re megkapjuk a képtéri fókusztávolságot:
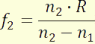 (4.5)
(4.5)
p2 = ∞-re pedig az f1 tárgytéri fókusztávolság
adódik:
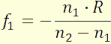 (4.6)
(4.6)
Visszahelyettesítve (4.4)- be a fókusztávolságokat kapjuk a képalkotási egyenletet:
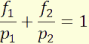 (4.7)
(4.7)
összeadva a 4.5 és 4.6 paraxiális esetben levezetett
összefüggéseket kapjuk, hogy:
f1
+ f2 = R (4.8)
Az f1 és f2 arányára pedig igaz, hogy:
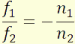 (4.9)
(4.9)
A csomópontok helyzete a 3. és 4.8 összefüggések alapján:
P1N1
= P2N2 = f1 + f2 = R (4.10)
A gömb törőfelület nagyításai:
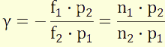 (4.11)
(4.11)
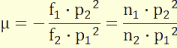 (4.12)
(4.12)
(4.9) alapján a törőfelület átellenes oldalain találhatók a fókuszpontok.
A törőfelület gyűjtő, ha f2 > 0, ez két esetben
is fenn áll:
- R > 0 és n2 > n1
a ritkább közeg felől domború a törőfelület
- R < 0 és n2 < n1
a tárgyoldali sűrűbb közeg felől homorú törőfelületre esik a fény .
4.2 Gömbtükrök
Gömbfelületű fényvisszaverődést
eredményező optikai rendszerek. A fényvisszaverődés
törvényéből az i1 = -i2
összefüggést a Snellius – Descartes töréstörvénybe
helyettesítve kapjuk, hogy n1 = -n2.
Ezzel a törésmutató értékpárral formálisan
fénytörésként kezeljük a fénytörést
és felhasználva a gömb törőfelületre kapott
összefüggéseinket kapjuk a gömbtükrök képalkotására érvényes
összefüggéseket:
(4.2) ⇒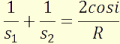 (4.13)
(4.13)
(4.3) ⇒ 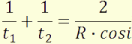 (4.14)
(4.14)
(4.4) ⇒ 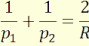 (4.15)
(4.15)
(4.5) ⇒ 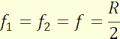 (4.16)
(4.16)
A gömbtükör paraxiális nyalábra
vett fókuszpontjai a tetőponttól a sugár felének megfelelő távolságra vannak.
(4.7) ⇒ 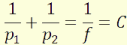 (4.17)
(4.17)
Nagyításai:
(4.11)⇒ 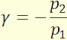 (4.18)
(4.18)
(4.12) ⇒ 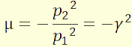 (4.19)
(4.19)
A mélységi nagyítás modulusa a vonalas nagyítás négyzetével
egyenlő, ami a kép erős torzulására utal.
A gömbtükör lehet domború és homorú aszerint, hogy milyennek tűnik a tárgytérből
nézve.
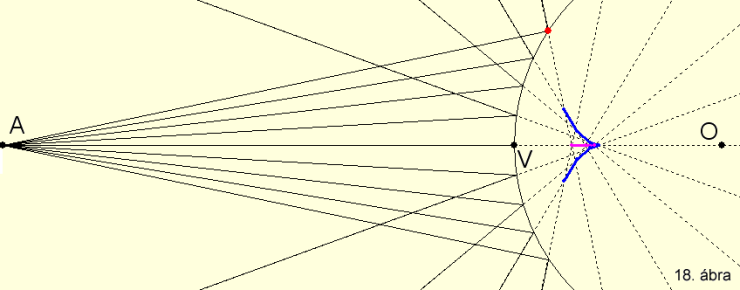
A 18. ábra alapján a domború tükör szór, általános
esetben nem alkot sztigmatikus képet, a lila szakaszban keletkezik az A pont
szagittális képe, a kék vonalak a tangenciális kép optikai tengelyt tartalmazó
síkmetszetét szemléltetik. (KSEG file
letöltése itt).
Paraxiális megközelítésben fedésbe kerülnek a képek. Mivel a végtelenben
levő tárgyat a fókuszsíkba képezi le és ez R/2 távolságra van, gyakorlatilag
a képtér mélysége R/2. Ez a tulajdonság teszi lehetővé a domború gömbtükrök
visszapillantó tükörként való alkalmazását személygépkocsik esetében, áruházakban
a termékek láthatóságát biztosítja a biztonságiak számára. A mélységi erős torzulás
valamint a jelentős kicsinyítés miatt a visszapillantó tükörben a távolság becslése
pontatlan, emiatt a jármű távolabbinak tűnik.
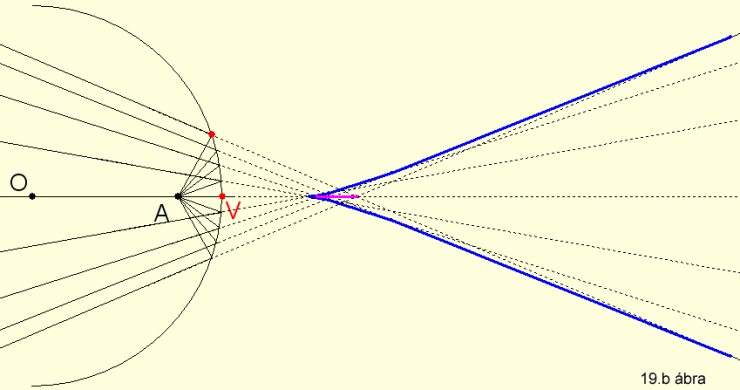
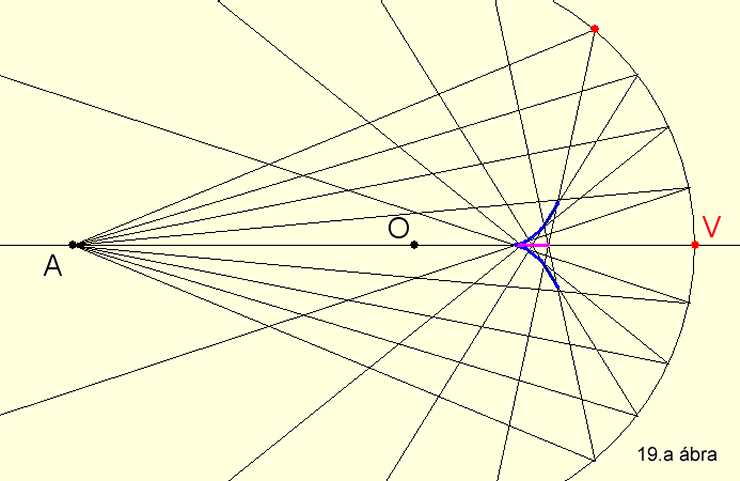
A homorú gömbtükör gyűjt és valódi képet alkot (19.a
ábra) (KSEG
file letöltése itt), amennyiben a tárgytávolság +∞
és f=R/2 között van, illetve szór és látszólagos képet alkot (19.b
ábra)
(KSEG file letöltése itt), ha a tárgy a fókuszpont és a V tetőpont között
található.
4.3 A sík törőfelület
Egyenleteit a gömb törőfelület egyenleteiből kapjuk R= ∞
-t behelyettesítve.
A szagittális képalkotás egyenlete:
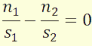 (4.20)
(4.20)
A tangenciális kép egyenlete:
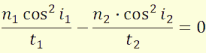 (4.21)
(4.21)
(4.4) alapján:
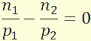 (4.22)
(4.22)
és mivel n1/n2 = p1/p2>0,
következik, hogy kép és tárgy a törőfelület ugyanazon
oldalán helyezkedik el. Valódi tárgyról látszólagos
képet alkot és a fénymenet megfordíthatóságából
adódóan látszólagos tárgyról valódi
képet. A ritkább optikai közegben levő tárgy távolsága
a törőfelülettől kisebb, mint a képtávolság.
Sűrűbb közegben levő tárgypont képe viszont ritkább
közegből szemlélve közelebb látszik. Ezért például
a vízzel telt medencében levő tárgy a felszínhez
közelebb látszik, a hatás a nagyobb mélységekre szembetűnőbb.
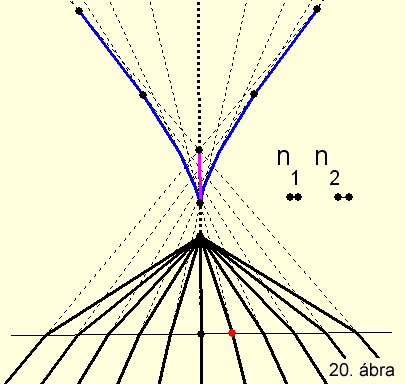 A 20. ábrán (KSEG
file letöltése itt) megfigyelhető, hogy általános esetben
nem sztigmatikus a leképezés. A ferdébben beeső sugarakra nagyobb a tárgy
– kép távolsága. A sík törőfelület
(vízszintes szakasz) a felső ritkább közeg egy pontjának
egy szagittális képszakaszt és egy tangenciális forgásfelszínnel
rendelkező képet feleltet meg.
A 20. ábrán (KSEG
file letöltése itt) megfigyelhető, hogy általános esetben
nem sztigmatikus a leképezés. A ferdébben beeső sugarakra nagyobb a tárgy
– kép távolsága. A sík törőfelület
(vízszintes szakasz) a felső ritkább közeg egy pontjának
egy szagittális képszakaszt és egy tangenciális forgásfelszínnel
rendelkező képet feleltet meg.
A lilával ábrázolt szagittális képszakasz a tárgypontból a határfelszínre merőleges
optikai tengelyen van.
A tangenciális képet az optikai tengelyt tartalmazó síkmetszetben kék színű
vonalak szemléltetik.
4.4 Síktükrök
A képalkotásra vonatkozó összefüggéseket a sík törőfelület
egyenleteibe való n1 = -n2 és i1
= -i2 behelyettesítéssel nyerjük:
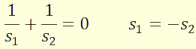 (4.23)
(4.23)
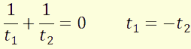 (4.24)
(4.24)
paraxiális megközelítésre:
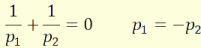 (4.25)
(4.25)
Nagyításai:
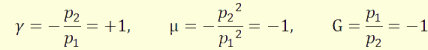 (4.26)
(4.26)
Az A tárgypont és A’ képe a síktükörtől
azonos távolságra helyezkedik el (21.a
ábra).
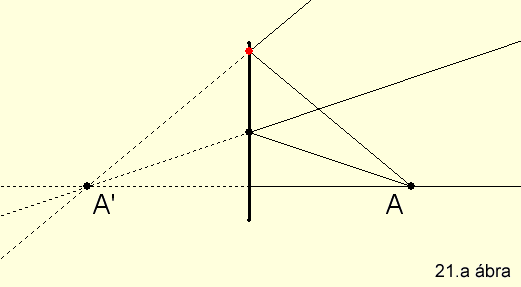
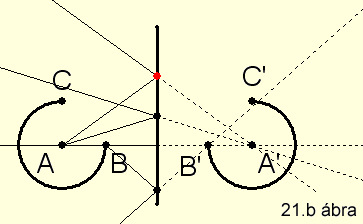
A tárgyról egyenes állású, mélységben fordított képet alkot. Mivel γ és
μ modulusa egyenlő a kép nem torzított, a leképezés sztigmatikus és aplanatikus
(21.b ábra) (KSEG
file letöltése itt).
4.5 Prizmák
Két egymással szöget bezáró sík törőfelület alkotja. Optikai
prizmák anyaga átlátszó. Jellemzőik az n törésmutató és az A törőszög, ez utóbbi
a két törőfelület által bezárt lapszög. A törőfelületek metszésvonalát törőélnek
nevezzük. A törőélre merőleges sík és a prizma keresztmetszetéből származik
a prizma főmetszetét jelentő háromszög. A prizma főmetszetének síkját és monokromatikus
fényt használunk a prizma képalkotásának tárgyalásához
(22. ábra)
(KSEG file letöltése itt).

A Snellius – Descartes töréstörvényét rendre
mindkét törőfelületre felírva i1 beesési
szögre meghatározható i2 értéke,
valamint a D eltérítési szög. NI1I2
háromszögben D külső szög és
értéke D=(i1-i’)+(i2-i"). Ugyanakkor
MI1I2 háromszögben A külső szög
értéke A= i’+ i". E két összefüggés
értelmében az eltérítési szög értéke:
D = i1 + i2
- A (4.27)
Az eltérítési szög adott törésmutató és törőszög mellett csak
a beesési szög függvénye. A 23. ábra A=60°
és n=4/3 értékre szemlélteti ezt a függvényt. Az ábra
alapján 42°-os beesési szög mellett a Dmin =
23.321°
A gyakorlatban a legkisebb eltérítési szögnek van
jelentősége, ez adott n, A értékek
mellett egyetlen beesési szög értékre teljesül,
éspedig amikor a prizma belsejében terjedő fénysugár
merőleges a törőszög szögfelezőjére.
Ebben az esetben i’= i"= A/2. Ez viszont i1 = i2
esetében valósulhat meg. Megállapítható,
hogy minimális eltérítéskor a fénymenet szimmetrikus
a törőszög szögfelezőjével. A beesési
szög értéke ez esetben:
i1m = (Dmin + A)/2
(4.27)
Az értéke viszont az eltérítési szög ismerete nélkül is meghatározható, mert
sin i1m=n·sin(A/2), innen pedig:
i1m = arcsin[n·sin(A/2)]
(4.28)
Ha egyenlővé tesszük a 4.27 és 4.28–as összefüggések
jobboldalait észrevehető hogy megoldás kínálkozik
a törésmutató meghatározására:
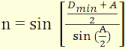 (4.29)
(4.29)
Ismeretlen anyag törésmutatójának
meghatározásához csiszolhatunk belőle egy A törőszögű
prizmát, monokromatikus fényt bocsátunk rá olyan
beesési szög mellett, hogy szimmetrikus fénymenet adódjon,
ekkor megmérjük az eltérítési szöget és
(4.29) –be behelyettesítve kiszámoljuk a törésmutatót.
Mivel sztigmatikus leképezés csak paraxiális nyalábra
áll fenn, ezért a színképelemző készülékre
eső nyalábot egyszer párhuzamosítják.
Optikai ékek azok a prizmák, melyek törőszöge nagyon kicsi, általában 0<A<10°
értékhatárok között változtatható. Kis beesési szögekre sin i1 =
i1 (rad). A töréstörvény az első törőfelületen i1 = n·i´,
a másodikon
i2 = n·i´´ alakra egyszerűsödik. Ezeket összeadva: i1+i2
= n(i´+i´´) ahonnan (4.27) alapján D+A = n·A. Az optikai ék eltérítési
szöge kis beesési szögek esetén:
D = A·(n-1)
(4.30)
A legtöbb optikai közegre D<A, ez lehetővé teszi az optikai
ékek felhasználását a sugármenet finom elforgatására és kis eltolására. Az eltérítés
fokmásodperces pontossággal beállítható. A 24. ábra
görbült felületük mentén érintkező, azonos görbületi sugarú, egymáshoz képest
elcsúsztatható síkhomorú és síkdomború lencse által alkotott változtatható törőszögű
éket szemléltet.
4.6 Lencsék
Két törőfelület által határolt optikai rendszer, amelyből legalább
egyik gömb törőfelület.
Forgástest melynek szimmetriatengelye az optikai tengely. Amennyiben a forgástengellyel
egyenközű párhuzamos síkokkal metszenénk, a szomszédos síkmetszetek közötti
elemi prizmák halmazaként lehetne felfogni. Az elemi prizmák törőszöge csökken
a tengelytől távolodva. Az optikai tengellyel párhuzamosan beeső sugarak a tengelytől
való távolság függvényében más-más törőszögű elemi prizmára esnek (23.
ábra).
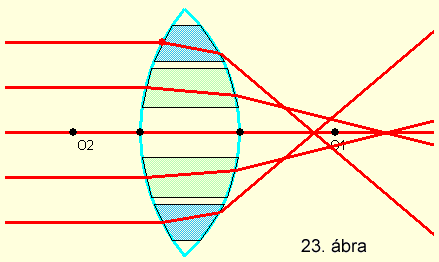 Nagyobb törőszögűek a tengelytől távolabbi elemi prizmák.
A nagyobb törőszögnek viszont nagyobb eltérítési szög felel meg, ezért a lencse
a csúcsához közeli sugarakat erősebben téríti el.
Nagyobb törőszögűek a tengelytől távolabbi elemi prizmák.
A nagyobb törőszögnek viszont nagyobb eltérítési szög felel meg, ezért a lencse
a csúcsához közeli sugarakat erősebben téríti el.
Geometriájuk alapján a középen vastagabbak gyűjtő- (konvex), a középen vékonyabbak
pedig szóró (konkáv) lencsék. Általános esetben az n törésmutatójú lencse törőfelületei
n1, illetve n2 törésmutatójú közegekkel határosak. A törőfelületek
görbületi sugarait pozitívnak vesszük, amennyiben görbületi középpontjaik a
tetőpontjuktól jobbra vannak. A V1V2 = e
távolság a lencse optikai tengely menti vastagsága. A centrált rendszereknél
levezetett összefüggések értelmében ´ tárgyoldali-, ´´
képoldali mennyiségre utal.
A lencse fókusztávolságaira fennálló összefüggések:
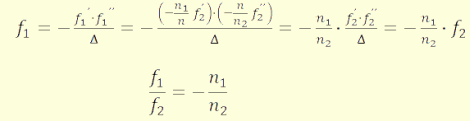 (4.31)
(4.31)
A 4.31-es összefüggés értelmében a lencse fókusztávolságainak
aránya független a lencse anyagának törésmutatójától. Ha mindkét törőfelületét
ugyanaz a közeg veszi körül, akkor a fókusztávolságok csak előjelben különböznek,
ami azt jelenti, hogy a lencse átellenes oldalán van a két fókuszpont.
Vékony lencse esetében e≈0, gyakorlatilag egybeesnek a fősíkok. Ha mindkét
oldalról ugyanazzal a közeggel határos, akkor a lencse fókusztávolsága:
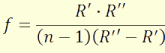 (4.32)
(4.32)
Ha egyik oldala, például a tárgy felöli, sík
törőfelület, akkor R’→∞ és f előjele
-R" előjelével egyenlő, emiatt a síkdomború
lencsének valódi-, a síkhomorúnak pedig látszólagos
a képtéri fókusztávolsága.
Képalkotási egyenletei:
x1·x2 = -f2
(4.33)
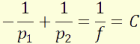 (4.34)
(4.34)
Nagyításai:
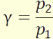 (4.35)
(4.35)
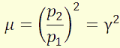 (4.36)
(4.36)
4.7 Lencserendszerek
Közös optikai tengely mentén elhelyezkedő lencsékből áll. Az
egyesített centrált rendszerekre vonatkozó összefüggések értelmében az egymástól
d távolságra levő f´ és f´´ képtéri fókusztávolságú vékonylencse-rendszer optikai
köze:
Δ = f´´- d +f´
(4.37)
Képtéri fókusztávolsága:
f=(f´·f´´) / (f´+f´´-d) (4.38)
Tárgyoldali gyújtósíkjának távolsága a tárgyfelőli lencse fősíkjától:
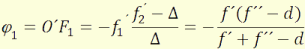 (4.39)
(4.39)
A képoldali fókuszsík távolsága a második lencsétől
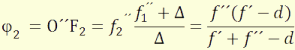 (4.40)
(4.40)
Fősíkjainak a helyzete:
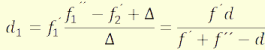 (4.41)
(4.41)
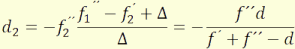 (4.42)
(4.42)
Afokális lencsepárra:
d = f´ + f´´.
A rendszer törőképessége:
C = C´ + C´´ - d.C´C´´
(4.43)
Illesztett vékonylencse-párra, d=0.
C = C´ + C´´
(4.44)
5. KÉPHIBÁK
Az egyszerű optikai rendszerek tanulmányozása során láttuk,
hogy sztigmatikus leképezésre csak a síktükör alkalmas. A tökéletes leképezéstől
való eltérést nevezzük képhibáknak. A képhibák két csoportba sorolhatók: színi
hibák és geometriai hibák.
A színi hibákat a diszperzió okozza, emiatt a tükrök mentesek e hibától, mivel
a fényvisszaverődés független a fény hullámhosszától.
A geometriai képhibákat a sugármenet és az optikai rendszer geometriai sajátosságai
okozzák. Láttuk, hogy többnyire csak paraxiális megközelítésben lehet elfogadható
képet létesíteni.
5.1 Színi hibák
A különböző hullámhosszaknak megfelelő, eltérő törésmutatókhoz
más-más fókusztávolság tartozik, ami a képalkotási összefüggések alapján eltérő
helyzetű és méretű képeket eredményez.
A képek helyzeti színi hibáját a C és F színképvonalaknak
megfelelő fókusztávolságok F2CF2F
különbségén keresztül értelmezik. A 9.
ábra alapján a törésmutatók
különbsége körülbelül 0,15-0,2, ez mintegy 11-15%-nak
felel meg üveg esetében, ekkor a fókusztávolságok
közötti eltérés 10% körüli. A 25'.
ábra vékony lencse képalkotásán
keresztül szemlélteti a helyzeti színi hibát.
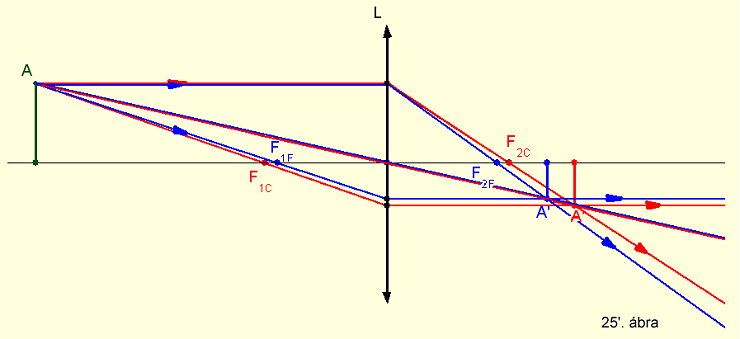
Megfigyelhető, hogy kék színben nagyobb
a vonalas nagyításunk. A nagyításban való
eltérést nagyítási színi hibának nevezzük.
Az F2F gyújtópontban az optikai tengelyre merőleges
ernyőn kék folt vörös körvonallal, illetve az F2C
–be hasonló módon helyezett ernyőn vörös
folt kék szegéllyel jelenik meg. A színi hiba csökkentése
illesztett lencsepárok (szóró- és gyűjtő
lencse ellentétes irányítású színi
hibát eredményez) segítségével és
a hasznos nyaláb nyílásszögének szűkítésével.
5.2 Geometriai képhibák
5.2.1 A nyíláshiba
Az optikai tengellyel párhuzamosan beeső sugarak a rendszerből
kilépve más-más helyen metszik azt, tehát a gyújtótávolság a tengelytől való
távolság függvénye. Az ebből adódó leképezési hibát nevezik nyíláshibának vagy
gömbi eltérésnek. A vastaglencséknél megfigyelt képalkotásból kitűnt, hogy ez
a hiba a görbületi sugár csökkenésével növekszik és lencse anyagának relatív
törésmutatójával is együtt nő.
5.2.2 Az asztigmatizmus
Az
optikai tengellyel viszonylag nagy szöget bezáró szűk nyílásszögű nyaláb leképezése
okozza az asztigmatizmust. Egy tárgypontból két egymásra merőleges síkban haladó
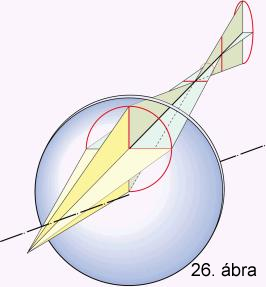
optikai rendszerre eső sugaraknak más-más képpontok felelnek meg. A 26.
ábrán megfigyelhető, hogy a meridionális síkban (a főtengely
és a tárgypont által meghatározott) levő fonálkereszt függőleges-, valamint
a meridionális síkra merőleges síkban fekvő vízszintes szakasza különböző képtávolságra
és ebből adódóan különböző nagyítással képeződik le.
5.2.3 A képgörbület
Abban nyilvánul meg, hogy egy síkfelületet görbe felületbe
képez le az optikai rendszer. A vastaglencse meridionális síkjában levő kék
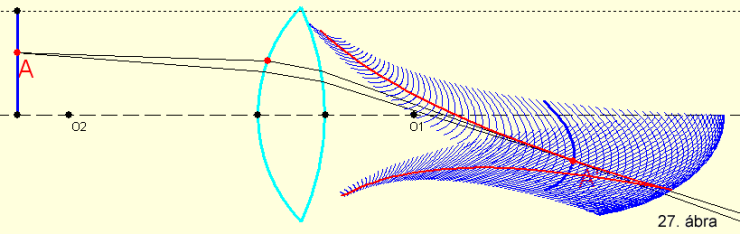
tárgyszakaszról alkotott görbe vonalú kép a 27. ábrán
figyelhető meg.
5.2.4 A torzítás
Egy tárgy felületén a szomszédos pontok által meghatározott
szakaszokra eltérő vonalas nagyítás adódik a nyíláshiba következményeként, ez
a kép torzulását vonja maga után. A 26. ábra
vastaglencse képalkotási hibáit szemlélteti az optikai tengelyt és a rá merőleges
tárgyat magába foglaló meridionális síkban. A tárgyat jelentő szakasz képe erősen
görbült. Itt a torzítás azért olyan nagymértékű, mert az optikai tengellyel
nagy szöget bezáró A-ból kiinduló szűk nyílásszögű nyaláb hozta létre. A képtérben
a piros görbe vonal az A pont képének mértani helye, miközben A-ból (r) kiinduló
szűk nyílásszögű nyalábbal pásztáztuk a lencsét. A kék görbesereg a lencse különböző
tengelytől mért távolságra levő részeinek tárgyról alkotott képe. A lencse felső
széle által alkotott kép a felső térrészben keletkezik, kicsinyített és a lencséhez
közel van. A legtávolabbi és legnagyobb képet a lencse közepe alkotja. Észrevehető
hogy a tárgy talppontjának a képe csak a lencse közepére eső nyaláb esetében
van az optikai tengelyen. Egy négyzet képe hordó alakú, ezért hordó alakú torzításról
beszélünk. Fordított képmenetet alkalmazva és figyelembe véve, hogy a lencse
közepe fele egyre nagyobb a nagyítás a négyzet képe párna alakú lesz, ez a párna
alakú torzítás. A torzítást százalékban fejezik ki: Δγ/γ ·100%.
5.2.5 A kóma
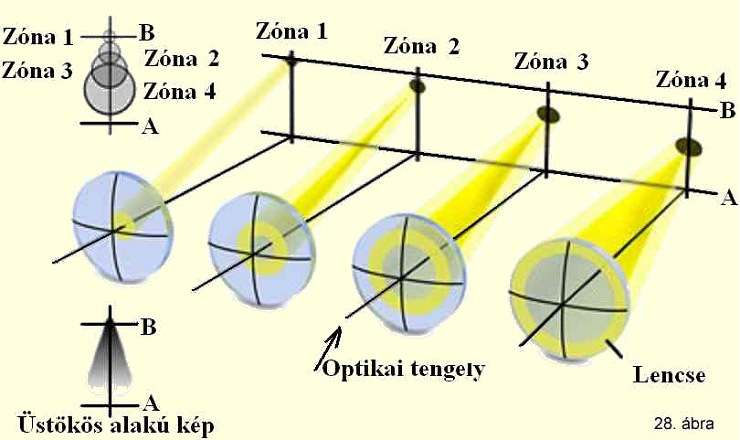
Üstökös alakjához hasonlatos képhiba.
Az optikai tengellyel nagy hajlásszöget bezáró, nagy
nyílásszögű nyaláb leképezésekor
jelenik meg. A 28. ábra az optikai
tengellyel nagy szöget bezáró párhuzamos sugárnyaláb
leképezésekor létrejövő kóma létrejöttére
ad szemléletes magyarázatot. A tengelyre merőlegesen elhelyezett
ernyőn a képzeletben négy szomszédos zónára
osztott lencserészek leképezése látható.
Az ernyő az 1-es zóna fókuszsíkjával csaknem
egybeesik. A lencse közepétől távolodva a rendre következő
külsőbb zónák fókuszsíkjai közelebb
vannak, emiatt elmosódottabb, nagyobb, az optikai tengelyhez közelebbi
foltok felelnek meg nekik.
III. SZÁMÍTÓGÉPES SZIMULÁCIÓK A GEOMETRIAI
OPTIKÁBAN
A számítógépes szimulációk lényegében olyan modellek, amelyek
segítségével bizonyos jelenségek lényegi elemeinek, paramétereinek függvényében
lehetővé válik egy rendszer várható viselkedésének tanulmányozása. Tágabb értelemben
véve szimulálni annyit tesz, mint másolatot készíteni a rendszer lényegéről,
anélkül, hogy a rendszert vagy tevékenységet ténylegesen érintenénk. Minél jobb
a modell, annál pontosabban írja le a valódi jelenséget.
Manapság a számítógépes modellezés a technikai fejlesztésnek legalapvetőbb eljárása.
Számítógépeink sebessége olyan mértékben megnőtt, hogy hamarabb elvégeznek egy
műveletet, mint amennyi idő alatt monitorunkról szemünkbe jut a fény. Egy 3GHz-es
processzor egy elektronikus mikrokapcsoló 3·109 nyitogatására
képes másodpercenként, míg a fény 10 cm-es távolságot tesz meg egy kapcsoló
nyitogatásnyi idő alatt. Így rengeteg idő takarítható meg.
A fizika oktatásában jelentősen megnövekedett a szerepük, mert lehetővé teszik
a tanteremben, laboratóriumban be nem mutatható jelenségek, el nem végezhető
kísérletek modellezését. Magreakciókat például csak szimulációkon keresztül
láttathatunk.
A számítógépes modellezést szoftverek teszik lehetővé. Ezek a programok három
csoportba oszthatók:
szabadon letölthető korlátozott ideig vagy megszorításokkal használható shareware-ek,
licensz azaz használati jogdíj megvásárlásával a korlátozás feloldódik ingyenesen
letölthető nem korlátozott freeware-ek weblapon megtekinthető, ott futtatható,
de nem letölthető programok.
Könnyű belátni, hogy jogtiszta felhasználás érdekében otthoni alkalmazásra a
leginkább a freeware típusúak alkalmasak.
6. SZIMULÁCIÓK A FIZIKA ÓRÁN
Az oktatásban általánosan elfogadott álláspont szerint a legeredményesebb
oktatási stratégia az aktív módszerek használata. Az aktív módszer ismérve,
hogy a diák feldolgozója, értelmezője az elsajátítandó ismereteknek, tanári
útmutatás mellett újra felfedezi, feltárja a jelenségek ok-okozati törvényszerűségeit.
A fizika órán alkalmazható aktív módszerek közül a leghatékonyabb a kísérletezés.
A demonstrációs kísérlet tanár által bemutatott, a tanulói kísérletet a diákok
végzik tanári felügyelet mellett. Típusát tekintve mindkettő lehet kvalitatív
vagy kvantitatív.
A kvalitatív kísérlettel egy fizikai jelenség megfigyelése, elemzése és minőségi
összefüggéseinek feltárása valósítható meg.
Kvantitatív kísérletezéskor méréseket végzünk, a mérési eredmények közötti összefüggések
alapján új mennyiségeket értelmezünk, törvényeket fogalmazunk meg.
A kísérletezés alkalmazható új tananyag feldolgozásában, elsajátított ismeretek
elmélyítésében.
A számítógépes modellezés, szimuláció kiegészítheti a kísérletezést, vagy lehetőséget
ad olyan jelenségek bemutatására, amelyre nem kínálkozik kísérletezési lehetőség.
Amennyiben a kísérletezés lehetősége adott, azt mindenképpen el kell végezni.
A laboratóriumi felszerelésben a drágább eszközök (oszcilloszkóp, jelgenerátor,
légpárnás mechanikai kísérletek) korlátozott számú előfordulása csak demonstratív
kísérlet bemutatását teszi lehetővé. A geometriai optikában is adódnak hasonló
helyzetek, optikai táblából és párhuzamos nyalábú lézer fényforrásból mindössze
egy van, így például a lencsékkel korrigálható szemhibák csak demonstratív kísérletezéssel
mutathatók be. A demonstratív kísérlet kiegészíthető az informatika teremben
vagy akár otthon elvégzett szimulációval.
A szimuláció egyedülállóan használható
olyan jelenségek tanulmányozására, amikor egyáltalán
nincs lehetőség kísérleti feldolgozásra a
kísérleti eszköz hiánya, a jelenség veszélyessége
és nem utolsó sorban a jelenség lejátszódási
időtartamának nagyon kicsi vagy éppenséggel nagyon
nagy volta miatt. Szimulálhatunk például láncreakciót,
rövidzárlatot, spektroszkópiát, Brown-féle
hőmozgást, kondenzátor feltöltődést
– kisülést, elektrolízist stb.
A számítógépes szimuláció feldolgozható:
- demonstratív módon, tanár által bemutatva
- tanulók által frontálisan az informatika teremben
- otthon
6.1 Tanár által bemutatott demonstratív szimuláció
Demonstratív bemutatás történhet vetítővászonra vagy interaktív
táblára való vetítéssel. A számítógép kijelzőjén megjelenő tartalmat egy digitális
projektoron keresztül kivetítjük így az egész osztály számára megfigyelhető
lesz a szimuláció. A szimuláció előtt hipotézisek megfogalmazására késztetjük
a diákokat, ezáltal biztosítjuk az aktív részvételt.
Egyszerű vetítő vászon esetében a tanár a szimulációt a számítógépen keresztül
irányítja, magyarázattal egybekötötten szemléltet, megfigyelési szempontokat
ad meg. Figyelem irányító eszközként használhatjuk az egérmutatót. A tanár az
osztállyal szemben helyezkedjen el, ez növeli a magyarázat hatékonyságát és
biztosítja az azonnali visszacsatolást.
6.2 Tanulók által frontálisan végzett
szimuláció
A frontálisan végzett szimulációk színhelye az informatika
terem, AEL terem lehet.
A tananyag feldolgozás szempontjait megadja a tanár, a diákok saját ritmusuknak
megfelelően haladhatnak. A tanári beavatkozás egyénre szabott lesz. Feladatlappal
egybekötve ajánlott a szimulációt végezni. A feladatlappal visszajelzést kapunk
a feldolgozás szintjéről és elkerülhetjük, hogy a diák rendszertelenül, felületesen
dolgozzon vagy egyébbel foglalkozzon.
Az AEL platform kivételt képez a feldolgozás módját illetően. Úgy dolgozták
ki, hogy egy tanítási egységen belül kis lépésekben egyéni ritmusban halad a
diák, viszont tanítási egységet tanári beavatkozást követően egyszerre váltanak.
Így frontális magyarázattal egybeköthető a tanítási egység feldolgozása.
A visszacsatolást biztosíthatja maga a program is. Általában feleletválasztásos
űrlappal mérhető a megértés szintje. Jó válasz esetén továbbléphet a diák, hibás
válasz esetén visszaküldik a dokumentálás helyére.
6.3 Otthon végzett szimulációk
Egyéni kísérletezésre, szimulációra azért van szükség, hogy
a meglévő ismereteinket felelevenítsük, alkalmazási szintre fejlesszük. A megértés
és alkalmazás sok esetben nagyon távol esik egymástól. Amit értünk nem feltétlenül
tudjuk is. A tudás igazi záróköve az alkalmazás.
Ingyen letölthető szimulációs programokkal fejleszthetjük tudásszintünket, a
többféle modell lehetőséget nyújt összehasonlításra, analízisre. A vektorgrafikai
szimulációk programozási ismeretek nélkül is lehetőséget kínálnak új modellek
kidolgozására a geometriai fénytan tárgykörében.
A szimuláció segíthet házi dolgozat elkészítésében, feladat megoldásában. A
tanár számára is lehetőséget kínál érdekes feladatok megfogalmazására. A kvantitatív
és kvalitatív szimulációk gyorsan elkészíthető, egyénre szabott feladat kidolgozásokat
tesznek lehetővé, ezzel a differenciált oktatás igénye is kielégíthető.
A szimuláció pozitív hozadékai:
- a matematikai modell csak a jelenség szempontjából lényeges elemeket
tartalmaz
- a paraméterek külön-külön változtatásával a törvényszerűségek jobban
megfigyelhetők
- a szimulációban használt színkódokkal kihangsúlyozhatóak az összefüggések
- mennyiségi összefüggések (kvantitatív modell) azonnal leolvashatók
- aktív tananyag feldolgozást feltételez.
7. MATEMATIKAI FÜGGVÉNYEK A FIZIKAI JELENSÉGEK
MODELLEZÉSÉBEN
A szimulációk matematikai modelleket használnak. Minél komplexebb
egy jelenség, annál több paraméter szükséges a leírására. A paraméterek változásait
matematikai függvények írják le. A legegyszerűbb dinamikai modellben csak egy
paraméter változik egy másik függvényében. Az egyenesen arányos mennyiségek
elsőfokú polinomiális függvényekkel leírhatók. Ilyen egyváltozós lineáris függvény
számos fizikai jelenséget leíró törvényben megjelenik. Egyenes vonalú egyenletes
mozgás esetén például az út-idő függvényét az x(t) = x0 + v·(t
- t0), egyenes vonalú egyenletesen gyorsuló mozgásnál a sebesség-idő
függvényét a v(t) = v(t0) + a·(t - t0) egyenes
egyenlete írja le.
A centrális erőtérben mozgó test pályáját leíró matematikai függvény egy kúpszelet
egyenes, kör, ellipszis, parabola, hiperbola egyenlete lehet.
Periodikus jelenség egyes paramétereinek (helyzet, sebesség, gyorsulás) időbeni
változása sinus, cosinus trigonometriai függvényekkel fejezhető ki.
Exponenciális függvények írják le például
egy kondenzátor feltöltődését – kisülését.
Logaritmikus függvény adja meg például a rakéta, mint változó tömegű rendszer
sebességének alakulását tömege függvényében v = vex·ln(m0
/ m).
A függvény adott értelmezési tartományon való viselkedése alapján előrevetíthető
a jelenség lejátszásának módja.
A függvényértelmezésben az alábbi matematikai fogalmaknak van jelentős szerepe:
folytonosság, szingularitás, gyökök, szélsőérték, határérték, meredekség, érintő,
inflexiós pont.
Folytonos függvény alatt azt értjük, hogy értelmezési halmazának minden pontjában
folytonos, nincs szakadási pontja. Szingularitásai akkor vannak egy függvénynek,
ha vannak olyan pontjai, amelyeknek nem felel meg jól meghatározott érintő vagy
érintősík. Például az 1/x függvény 0-ban szinguláris, mert végtelent ad a nulla
behelyettesítési értékére.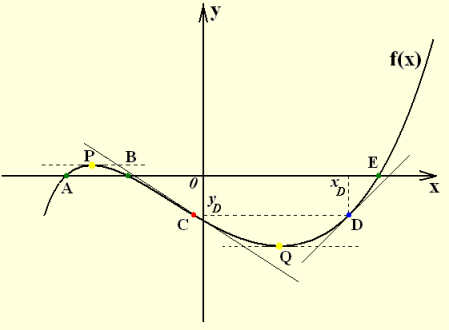
A függvény gyökei azok a számok, amelyekre a függvény értéke zéró. A mellékelt
ábrán az A, B és E-vel jelölt pontokban a függvény értéke zéró, tehát xA, xB
és xE a függvény gyökei.
Szélsőérték alatt egy függvény lokális minimumát vagy maximumát értjük. A szélsőérték
meghatározásához deriváljuk a függvényt és ennek a gyökei adják a függvény
szélsőértékét. A függvényhez egy pontba húzott érintőnek a meredeksége jelenti
a függvény deriváltját az illető pontban. Amennyiben a derivált értéke itt zéró,
akkor hozzá vízszintes érintősík tartozik, ez a lokális szélsőérték feltétele
folytonos függvényre. A fenti ábrán a P, Q, C és D pontokhoz húzott érintők
vannak feltüntetve. P-hez és Q-hoz vízszintes érintő tartozik, P lokális maximum,
Q lokális minimum hely. A másodrendű derivált előjele alapján dönthető el, hogy
a szélsőérték helyi maximumot vagy minimumot jelent. Ha f(x) az (x0, y0) pontban
legalább kétszeresen deriválható és x0-ra f´(x0) = 0 valamint
f´´(x0) < 0, akkor lokális maximuma van a függvénynek f(x0)
= ymax, viszont ha f´´(x0) > 0 akkor lokális minimuma,
f(x0) = ymin. Amennyiben f´´(x0) = 0 és előjelet
vált x0 környezetében, akkor az f(x) függvénynek x0-ban
inflexiós pontja van. A fenti ábrán C inflexiós pont, a hozzá tartozó érintő
e pontban metszi a függvény képét.
A jelenségek matematikai értelmezése a változásukat leíró függvények segítségével
történik. A függvénykapcsolatok sem mindig egyértelműek, a mérési eredmények
alapján következtetik ki. Egyik módszer a mérési adatoknak megfelelő függvény
megtalálására a legkisebb négyzetek módszere. Ez akkor használható, ha ismert
a függvény, de a paraméterei nem. Például (xi,yi) pontpárok
adottak és tudjuk, hogy y=bx+a lineáris kapcsolatban vannak, de a és b paraméterek
nem ismertek. Az a és b paramétereket úgy kell tehát meghatározni, hogy az yi-y
eltérés négyzetének várható értéke minimális legyen, azaz S = M[(yi-bxi-a)2]
= min. A  egyenletrendszert megoldva meghatározható a és b paraméterek értéke.
egyenletrendszert megoldva meghatározható a és b paraméterek értéke.
 Határozott integrállal egy folytonosan változó függvény által
meghatározott vonalhosszat, területet vagy térfogatot számítunk ki. Ha például
az erő változik az x koordináták szerint, akkor az xA, xB
intervallumon való elmozdulás során végzett munkája az F(x) függvény grafikus
képe és az Ox tengely közé eső területtel egyenlő (a mellékelt ábrán a szürke
terület),
amit az
Határozott integrállal egy folytonosan változó függvény által
meghatározott vonalhosszat, területet vagy térfogatot számítunk ki. Ha például
az erő változik az x koordináták szerint, akkor az xA, xB
intervallumon való elmozdulás során végzett munkája az F(x) függvény grafikus
képe és az Ox tengely közé eső területtel egyenlő (a mellékelt ábrán a szürke
terület),
amit az 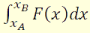 integrállal
számolunk ki.
integrállal
számolunk ki.
Amennyiben egy paraméter több időben változó paraméternek egyidejű függvénye,
a jelenség differenciálegyenlet formájában modellezhető. Például a mechanikában,
az esőcsepp mozgásegyenlete egy másodrendű differenciálegyenlet: 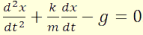 .
A súrlódási erő a sebességgel arányos (k·dx/dt), tehát a csepp gyorsulása
is változik.
.
A súrlódási erő a sebességgel arányos (k·dx/dt), tehát a csepp gyorsulása
is változik.
A differenciálegyenleteknek végtelen sok megoldása lehet. A kezdeti értékek
megadásával és egyéb megkötöttségekkel (kényszerek) viszont konkrét megoldások
adódnak. A kezdeti feltételek nagyon érzékennyé teszik a jelenség lefolyásának
a módját. Például szabadesés adódik nulla kezdeti sebesség mellett, függőleges
hajítás, ha a gyorsulás és sebesség iránya megegyező, ballisztikus hajítás,
amennyiben sebesség és gyorsulás iránya nem párhuzamos. Elegendően nagy kezdeti
sebességgel elhagyhatjuk a Földet (első kozmikus sebesség), a második kozmikus
sebességgel indított test már a Naprendszert is elhagyja.
általános esetben a matematikai leírásmód felettébb elbonyolódik
az inhomogenitások és soktényezős változások miatt. A légköri
jelenségek tanulmányozásához már káoszelméleti ismeretek szükségesek.
Az atomok, szubatomi részecskék kvantumos viselkedésű,
„furcsa” világában a kvantum mechanika, kvantum elektrodinamika
sajátos matematikai apparátusa írja le a jelenségeket.
Az iskolai fénytanoktatásban viszont a felsőbb matematika módszerei
integrálok, differenciálegyenletek nem jelennek meg, így homogén optikai közegekre
és Gauss-megközelítésben egyszerű matematikai apparátussal számíthatók a képalkotásra
jellemző fizikai paraméterek. A geometriai optika területén a vizuális modellek
készítésének van kiemelkedő szerepe, amit egyszerű vektorgrafikai alkalmazások
is képesek betölteni.
Vektorok
Vektor alatt irányított szakaszt értünk, tehát a vektor egy olyan mennyiség,
amelyet két egymástól független változó határoz meg: nagyság és irányítás.
xy síkban két a és b vektor megadható végpontjaiknak az origótól mért koordinátáik
segítségével. Ha egyik végpontjuk egybeesik az origóval, akkor az (xa,
ya) és (xb, yb) pontpárokkal
jellemezhetőek.
a nagysága (modulusa) |a|=(xa2+ya2)1/2,
és irányítása a nagyságát jelentő szakasz Ox tengellyel bezárt szögével Θa=arctan(ya/xa)
jellemezhető.
összegüket az a+b=(xa+ xb, ya+yb)
csúcs (végpont) koordinátái fejezik ki. Grafikusan
két vektor összegzése a paralelogramma-szabály szerint
történik. Egyik vektort a másikkal párhuzamosan toljuk,
amíg támadópontjuk egybeesik és a két vektor
képezi a paralelogramma egymás melletti oldalait és ugyanabból
a támadáspontból kiinduló átlója adja
az eredő vektort. (29. ábra)
(KSEG file letöltése itt)
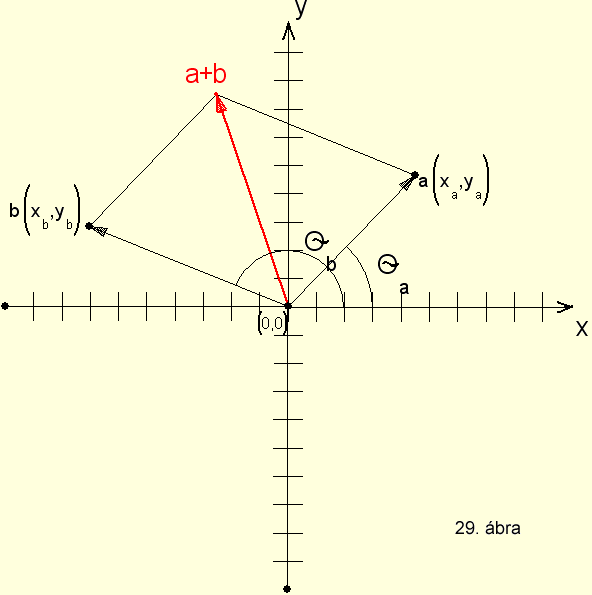
Egy vektort skaláris mennyiséggel szorozni annyit jelent mint koordinátáit a
skalárral egyenként beszorozni. Az origóból induló a vektornak k skalárral való
szorzásának eredménye egy új (k·xa, k·ya) csúcsú,
azonos irányítású, k-szoros nagyságú vektor.
Két a és b vektor skaláris szorzata skalárt eredményez a·b =
xa·xb + ya·yb.
Vektorszorzatuk eredménye egy olyan vektor, amelynek iránya merőleges a két
vektor által meghatározott síkra és irányítását a fúrószabály adja (az első
vektort forgatjuk a második irányába a közrezárt kisebb szög mértékében, ha
az óramutató irányába forgattunk az irányítás lefele mutat és fordítva). Ha
az xy síkban voltak a vektorok, akkor a z tengellyel párhuzamos a vektorszorzatot
kifejező vektor.
Nagysága a x b = |a|·|b|·sin(Θb-Θa).
A vektorok összeadása, skalárral való szorzása, skaláris szorzatuk kommutatív,
a vektorszorzat viszont antikommutatív (a x b = - b x a).
8. VEKTORGRAFIKAI ALKALMAZÁSOK
A vektorgrafikai programok vektoralgebrára támaszkodnak az
egyszerű geometriai ábrázolások elkészítésében. Legfontosabb grafikus elemeik
a pont, szakasz, egyenes, kör, körív. Minden grafikai objektum belőlük épül.
Külön-külön memóriarészt foglalnak le, ez lehetővé teszi tetszőleges kiválasztásukat
a rajzolás későbbi fázisaiban, különböző transzformációk (áthelyezés, átméretezés,
elforgatás, színezés, címkézés) alkalmazását rajtuk. Mivel valamennyi objektumot
néhány bázispont jellemez, ezeknek módosításai az egész objektumra kihatnak.
Két objektum metszeti pontjai vagy transzformációkból származó pontok viszont
nem bázispontok.
Vannak olyan vektorgrafikai programok, amelyek lehetővé teszik egy objektumból
új leszármaztatott objektum létrehozását bizonyos transzformációk által. Megkülönböztetünk
úgynevezett szülő-, illetve leszármazott objektumokat. A leszármazott objektumok
a szülőobjektumhoz kapcsolódó transzformációk révén létesültek. A szülőobjektum
azon részeinek módosítása, amelyek alapján leszármazottak keletkeztek, maga
után vonja a leszármazott módosulását is. Például ha egy négyzet két pontjával
értelmezünk egy vektort és ezzel a vektorral eltolunk egy kört, akkor a négyzet
átméretezése eltolja a kört a vektorral értelmezett nagyság és irány szerint.
Ez az egymásra épülés és kölcsönös összefüggés bonyolult kinematikai modellek
elkészítésére alkalmas.
8.1 A KSEG bemutatása
Az iskolában elvégzett szimulációk legtöbb esetben az iskolán
kívül nem hozzáférhetőek, ingyen sok esetben csak szerzői jogokat sértő módon
lehetne hozzájuk jutni. Ez alól kivételt képez a KSEG vektorgrafikai program.
A KSEG mértani ábrázolásra, szerkesztésekre alkalmas, így kiváló a geometriai
fénytan jelenségeinek szemléltetésére. Az euklideszi síkmértan szerkesztéseit
teszi lehetővé, ugyanakkor azonnali szög és távolság mérésekre is alkalmas.
A programot Ilya Baran írta 1996-ban saját szórakoztatására, mivelhogy sokallta
egy geometriai ábrázolás program 40 dolláros értékét. C++ projektként DOS-ra
írta az első verziót, Windows-ra a másodikat és mivel oktató szoftverként is
bevált és igény lett rá, Linux-ra is elkészítette.
A vonalzó és körző segítségével készíthető szerkesztéseket helyettesítő program
egy új dimenziót adott a mértani ábrázolásnak. A szerkesztések dinamikusak,
gyorsan és könnyen elkészíthetők, a változtatásokra azonnali a vizuális visszajelzés.
A program ablakot a 30. ábra
mutatja.
8.1.1 Geometriai objektumok
A szerkesztések a következő geometriai objektumokra épülnek:
Pont – jellemzői az (x,y) koordináták. A
rajzvászon (0,0) koordinátájú bal felső csúcsától
vízszintesen jobbra x és függőlegesen lefele y távolságokkal
jellemezhető.
Megkülönböztetünk szabad pontot és kötött pontot. A kötött pont egy vonalhoz
(egyenes, görbe) tartozik.
Szakasz – az (x1, y1) és (x2,
y2) végpontokkal értelmezett.
Szakasz felezőpontja – a szakasz végpontjai segítségével
értelmezett pont, koordinátái [(x1+ x2)/2,
(y1+y2)/2]. Szerkesztése a szakasz kiválasztásával
válik lehetővé
Félegyenes – kiindulópontja az (x1,
y1) elsőnek kiválasztott pont, irányítását
egy második pont helyzete határozza meg, amelyen keresztül
megy és végtelenben végződik.
Egyenes – két pont határozza meg, mindkét
vége végtelenben van.
Merőleges egyenes – egy kiválasztott egyenes (félegyenes,
szakasz, sugár) egy kiválasztott pontjára állított
merőleges.
Kör – az elsőnek kiválasztott pont adja a középpontjának
a helyzetét, a másodiknak kiválasztott pont adja a sugarának
végpontját.
Körív – három kiválasztott pont határozza
meg, az elsőnek és az utolsónak kiválasztott pont
jelenti az ív végpontjait.
Szögfelező – három kiválasztott pont alapján
szerkesztődik, a másodiknak kiválasztott ponton megy át
a szögfelező, az első pont a másodikkal valamint a
második a harmadikkal határozza meg a szögszárakat.
Mértani hely – egy kiválasztott leszármazott objektum
pályáját jelentő vonal, amelyet szülőobjektumának
lehetséges mozgása kelt. Feltétele, hogy a szülőobjektum
egy kiválasztott pontja egy vonalhoz (egyenes, félegyenes, szakasz,
kör) legyen kötve. Megszerkesztéséhez ki kell jelölni
a szülőobjektum futópontját és a leszármazottját.
8.1.2 Mérések
A program a következő mérési lehetőségeket kínálja:
Távolságmérés:
- két kiválasztott pont egymástól való távolsága,
- kiválasztott szakasz hossza,
- kiválasztott kör sugara
- kiválasztott körív hossza, kör kerülete
adható meg.
Szögmérés:
Három kiválasztott pont által meghatározott szöget ad meg körüljárásos irány
szerint. A második kiválasztott pont a szög csúcsát jelenti. A feltüntetett
szög ?, amennyiben az első kijelölt ponttól az utoljára kijelöltig a legrövidebb
úton az óramutató járásával ellentétes irányban jutunk vagy 3600-? ellenkező
esetben.
A mérési adatokkal egyszerű matematikai műveletek végezhetők (összeadás, kivonás,
szorzás, osztás, hatványozás, gyökvonás).
Területmérés
Zárt sokszögek, kör, körcikk, körszelet területét határozhatjuk meg.
8.1.3 Transzformációk
A transzformációk teszik lehetővé a dinamikusan együttmozgó,
együtt változó mennyiségek megjelenítését. Transzformációkkal az eredeti objektumoknak
leszármazottjai jönnek létre. Ezek azonos alakú és méretű példányok, egyedüli
kivételt a nagyítás jelent, amikor a méretek arányosan változnak.
Eltolás
Az eltolást egy vektor segítségével értelmezzük. A vektorunkat két kiválasztott
pont definiálja. Nagyságát a pontok távolsága, irányítását a kiválasztás sorrendje
határozza meg. Például az A és B pontok segítségével értelmezhetünk két vektort:
AB és BA = -AB -vektorokat.
Valamennyi kiválasztott objektum egyidejűleg eltolható. A kiválasztott objektummal
azonos másolat jön létre és ez tolódik el.
Tükrözés
Tükrözéshez egyszer egy szimmetriatengelyt értelmezünk. Szimmetriatengelyül
választható egyenes, félegyenes vagy szakasz. A tükrözés eredményeként a tengely
egyik oldalán levő objektumról, a síktükör képalkotásával azonos módon, a tengely
túloldalán, attól ugyanakkora távolságra keletkezik egy leszármazott másolat.
Forgatás
A forgatáshoz egy szöget és egy forgáspontot kell előre kijelölni. A forgatandó
objektumról keletkező leszármazott példány a forgáspont körül a kiválasztott
szögnek megfelelő mértékben és irányban fordul el. Szögharmadolás nem valósítható
pontosan meg körző és vonalzó segítségével. A program erre gyors lehetőséget
kínál. A választott szöget elosztjuk 3-mal majd a kiírt eredményt választjuk
ki a szög-transzformációhoz.
Nagyítás
A méretarányos nagyítási tényező két kiválasztott hosszúság hányadosa vagy egy
tetszőleges matematikai művelettel kapott eredmény is lehet. Ilyen esetben az
eredményt és az átméretezendő objektumot választjuk ki a nagyításhoz. Ha az
első kiválasztott szakasz hosszabb, akkor méretarányos kicsinyítést, fordított
esetben nagyítást eredményez a transzformációnk. Megjegyzendő, hogy azért nem
a szülő objektumon következik ez be, mivel annak méretei bármikor szabadon változtathatók
kijelölt részeinek mozgatásával.
A megjelenítés beállítható különböző nagyításokra. Külön ablakokban figyelhetjük
meg más-más kinagyított részek viselkedését, úgy hogy minden változtatás minden
ablakban egyidejűleg megjelenik. Ez leginkább akkor hasznosítható, amikor fedésbe
kerül több objektum, ilyenkor ugyanis a megfelelő objektum kiválasztása nehézkes.
Az objektumok megkülönböztetését megkönnyíti a színek használata, a különböző
címkézési lehetőségek, eltérő vonal vastagságok és stílusok. A segédszerkesztések
elrejthetők, ezáltal biztosított az áttekinthetőség. Az elrejtett szerkesztések
szükség esetén felfedhetők. Lehetőség van zárt alakzatokat színnel kitölteni.
A program legnagyobb kiaknázási lehetősége az automatizált szerkesztésekben
rejlik. Amennyiben úgy véljük, hogy adott szerkesztéseket később is alkalmazni
szeretnénk, elkészítjük új szerkesztésként, elmentjük és a Lejátszás menüpontból
bármikor meghívhatjuk őket, rengeteg időt megtakarítva. Ajánlott a program megismerését
követően elkészíteni gyakran alkalmazott szerkesztések makróit. Ilyen makrók
lehetnek például a vetületek körre vagy egyenesre, érintő, felezőpont, de ennél
sokkal bonyolultabb szerkesztések is elmakrózhatók, mint például a fénytörés
esetében a Weierstrass-szerkesztés.
8.1.4 Szerkesztések KSEG-ben
A szerkesztések alapjai a bázispontok.
Jobb egérgombos kattintással hozzuk őket létre a munkafelületen. CTRL+DELETE
kombinációval törölhető a kijelölt objektum. A program által alapértelmezett
szerkesztések a megfelelő kijelölések alapján hozhatók létre. Például, két kijelölt
pontra az eszközsor elvégezhető parancsikonjai aktívvá válnak (szakasz, félegyenes,
egyenes, kör, vektor, pontok távolsága). Egy egyenes kijelölése alapján meredekségének
kiszámítása aktivizálódik, illetve szimmetriatengelyként választható. Egy pont
és egy egyenes együttes kijelöléséből a program lehetőséget ad: a pont egyenestől
való távolságának megadására, a pontból az egyenesre merőleges-, vagy a ponton
keresztül párhuzamos egyenes szerkesztésére. Két vonal kijelölésére metszeti
pontjaiknak feltüntetése válik aktívvá még akkor is, ha nincs közös pontjuk
(mozgatásuk során metszhetik egymást).
A Weierstrass–szerkesztés
Az elméleti bevezetőben láttuk, hogy formálisan
még a fényvisszaverődés is a fénytörés sajátos eseteként kezelhető. A diszperzió
jelensége szintén fénytörésen alapszik. Képalkotó eszközeink a fénytörés és
fényvisszaverődés törvényein alapuló alkalmazások. Egyik legfontosabb szerkesztésünk
a képalkotásban a fénytörésre kidolgozott Weierstrass féle grafikus módszer
(31. ábra). (KSEG
file letöltése itt)
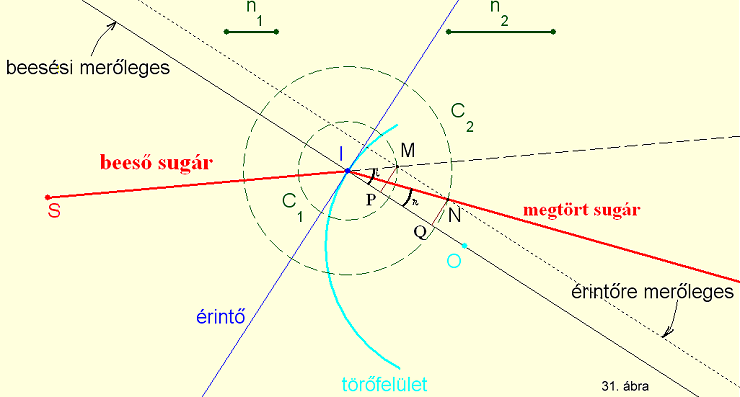
Az n1, n2 törésmutatóknak megfeleltetünk egy-egy szakaszt
(tulajdonképpen két pontpárt). Mindkét törésmutató tetszőlegesen változtatható
a szakaszok végpontjainak mozgatásával. A határfelületen felvesszük a beesési
pontot, e pontban megszerkesztjük az érintőt (görbült felszín) és a beesési
merőlegest. A törésmutatók nagyságát sugárként használva (rendre vektorként
értelmezzük őket, az I beesési pontot rendre eltoljuk a két vektor által, a
beesési ponttal és az eltolt pontokkal rendre köröket szerkesztünk) a beesési
pont, mint középpont köré két koncentrikus kört C1, C2
rajzolunk. Felveszünk egy S pontszerű fényforrást úgy, hogy ne legyen a határfelületen.
Az S fényforráson és az I beesési ponton áthaladó egyenes metszi mindkét koncentrikus
kört. Az első törésmutatót jelképező C1 kört a határfelület mindkét
oldalán metszi. A határfelület túlsó oldali M metszéspontjából merőlegest húzunk
a beesési pont érintőjére. A merőleges és a második közeget jellemző C2
kör határfelületen túli N metszéspontján fog a megtört sugár áthaladni.
A szerkesztés helyességének igazolására vetítsük a beesési merőlegesre az M
és N pontokat. A vetítés eredménye a P és Q pont. MP = NQ mivel két párhuzamos
egyenes közötti távolságot jelölnek. IMP derékszögű háromszögben sin i = MP/n1,
míg INQ derékszögű háromszögben sin r = NQ/n2. Tehát MP = n1
sin i és
NQ = n2 sin r, tehát n1 sin i = n2sin r.
A Weierstrass-szerkesztést
a gömb törőfelületre szokták megadni. Ahhoz, hogy tetszőleges felület bármely
pontjára alkalmazni lehessen célszerűbbnek láttam a beesési pont érintőjét tekinteni
lokálisan törőfelületnek.
Ahhoz hogy ezt a továbbiakban alkalmazhassuk, szerkesztésként is elmentjük.
A szerkesztésben adottá kell tenni a törésmutatókra jellemző pontpárokat a fényforrást
jelölő pontot, a beesési pontot valamint az érintőt. A gyakorlatban tehát úgy
alkalmazzuk ezt a szerkesztést, hogy a szerkesztésben adottá tevési sorrendet
betartjuk. Ha elsőként az első törésmutatóra jellemző pontpárt tettük adottá,
akkor a gyors lejátszásban is elsőként őket válasszuk ki. Mivel hat adott pontunk
van (4 a törésmutatókra, 1 a pontszerű fényforrásra, 1 a beesési pontra) ezért
a kijelölés sorrendjét szigorúan be kell tartani.
E szerkesztést alapul véve tekintsük meg a vastaglencse képalkotási szimulációjának
létrehozási módozatát.
Vastaglencsék képalkotásának szerkesztése
Felveszünk két pontot és az őket összekötő
egyenes lesz az optikai tengely. Beállítjuk vízszintesre és elrejtjük a két
pontot, ezáltal biztosíthatjuk, hogy az optikai tengely mindvégig vízszintes
helyzetű marad.
A lencse baloldali törőfelületét egy körív képezi (32.
ábra).
(KSEG-file
letöltése itt)
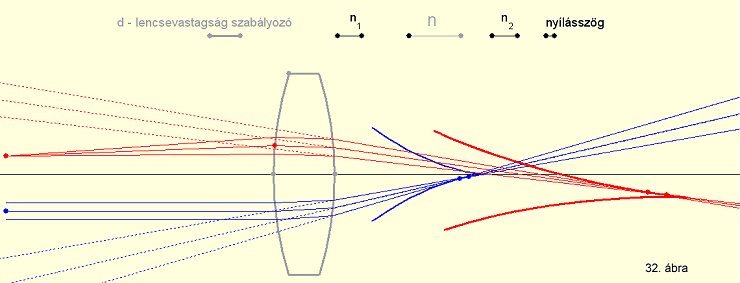
A körív szimmetrikusan kell elhelyezkedjen az optikai tengelyhez képest. A körív
szerkesztéséhez három pont kell. Ennek elkészítéséhez felveszünk egy pontot
a tengely felett, ez lesz a körív (lencse) egyik csúcsa (vége). Az optikai tengelyt
jelentő egyenest szimmetriatengellyé választjuk. A választás után tükrözzük
a tengelyen kívüli pontot, ezzel létrehozzuk a körív másik végét (átellenes
csúcs). A körív középpontja képezi a lencse V tetőpontját. A tetőpontot azonban
nem vehetjük fel tetszőlegesen a tengelyen, mert megtörténhet, hogy a csúcs
visszahajlik és nem lesz a törőfelület tengelytől legtávolabbi pontja. Ennek
elkerülésére a tetőpontot egy szakaszhoz kötjük. A szakasz megszerkesztésének
menete: A két csúcspontot egy egyenessel összekötjük. Az egyenes és az optikai
tengely metszéspontját feltüntetjük. Kört rajzolunk, a metszéspont lesz a kör
középpontja és az egyik csúcs a sugarát adja. A körnek a tengellyel való metszéspontjai
és a kör középpontja két kényszerítő feltételt jelentő szakaszt határoz meg.
Elrejtjük az optikai tengelyt, ezáltal biztosak lehetünk, hogy a tetőpontokat
a megfelelő szakaszokon vesszük fel. A két tetőpont felvétele után a szakaszokat
elrejtjük, majd az optikai tengelyt felfedjük. Immár adott mindkét törőfelület
megszerkesztésének lehetősége. A szerkesztésünk alkalmas bármilyen görbületi
sugár beállítására. Bármilyen típusú lencsét képezhetünk.
A képszerkesztésünk alapja a Weierstrass-szerkesztés. Ennek érdekében felvesszük
a törésmutatókat jelentő három szakaszt. Azért hármat, mert a legáltalánosabb
esetben a lencse törőfelületeit különböző közegpárok határozzák meg. Felvesszünk
továbbá egy tárgypontot és egy beesési pontot a tárgyoldali törőfelületen. A
beesési pontban érintőt szerkesztünk az érintő-makrót meghívva. Kiválasztjuk
a közegpárra vonatkozó törésmutatók pontpárait, a fényforrást jelentő pontot,
a beesési pontot és a hozzá tartozó érintőt majd meghívjuk a lejátszás menüből
az elmentett Weierstrass-szerkesztést. A megtört sugár metszi a második törőfelületet,
ez a pont lesz a következő beesési pont. Meghúzzuk a hozzá tartozó érintőt és
újból alkalmazzuk most már a következő közegpárra a Weierstrass-szerkesztést.
Ahhoz, hogy szabályozható nyílásszögű nyaláb essen a törőfelületre, értelmezünk
egy rövid vektort. E vektor segítségével eltoljuk az első beesési pontot. A
beesési pont és az eltolással létrehozott pont segítségével egy kört szerkesztünk.
A kör és a törőfelület két metszéspontja jelenti a szomszédos sugarak beesési
pontjait. Ezekre is hasonlóan járunk el a fénymenet megszerkesztésében. A baloldali
piros pontszerű fényforrásból kiinduló három sugármenetet figyelhetünk meg.
A lencsét elhagyó, egymás melletti fénysugarak metszéspontjaiban keletkeznek
a képek (asztigmatikus leképezés). A tárgyoldali törőfelületen végig futó beesési
pontot (szülő-objektum) és egy létrejött képpontot (leszármazott) együtt kijelölünk
és az Új menüpontból kiválasztva az új mértani hely parancsot, megkapjuk a fényforrás
tangenciális képét. Ezt a képtérben tölcsérszerű piros görbe szemlélteti.
Amennyiben a fókuszsíkok helyzetét szeretnénk megvizsgálni, akkor az optikai
tengellyel párhuzamos fénynyalábot bocsájtunk a lencsére. A párhuzamos nyaláb
fénymenetét kék vonal szemlélteti az ábrán. A fókuszsíkok mértani helyét a tangenciális
kép szerkesztésével analóg módon kapjuk. A fókuszsíkok mértani helyét a kék
tölcsér mutatja. A tetőpontba érkező nyaláb fókusztávolsága lesz abszolút értékben
a legnagyobb. Minél távolabb van az optikai tengelytől a nyaláb, annál közelebbi
fókuszsík felel meg neki.
A szimuláció sok érdekes dolgot tár fel miközben a paramétereit változtatjuk.
Megfigyelhető, hogyan változik a fókuszsíkok helyzete a görbületi sugarak változásakor,
ezt a tetőpontok mozgatásával érjük el. Észrevesszük, hogyan válik gyűjtőlencséből
szóró lencsévé, amint a lencse közepén vékonyabb lesz mint a szélein.
A lencse törésmutatóját a közegek törésmutatójánál kisebbnek véve a lencsénk
típust vált, gyűjtőből szóróvá vagy szóróból gyűjtővé alakul.
Szemléletesen derül ki továbbá az, hogy ugyanakkora nagyságú és előjelű görbületi
sugarakra is véges távolságra vannak a fókuszsíkok, tehát nem végtelenben mint
a vékonylencsék paraxiális közelítésében.
Még az optikai tengelyen levő pontok képei is csak a tetőpontba eső, szűk nyílásszögű
nyaláb esetében lesznek a tengelyen.
8.2 A program értékelése
Tartalmi kritériumok
A fénytani jelenségek matematikai modellezésében
elsősorban a dinamikus képi megjelenítésre alkalmas.
A KSEG-gel készült alkalmazások dinamikus szemléltetők szerepét tölthetik be.
Az approximációk nélkül megjelenített modellek, a geometriai optikának teljesebb,
mélyebb szintű megismerését teszik lehetővé. Az elmélet gyakorlatba ültetésének
kihívásai, nehézségei szembeötlő módon jelennek meg bennük. Számos, csak elméletben
megismert jelenségre, az elkészített modellek révén feltárul a lehetséges alkalmazás,
ami az ismeret leghatékonyabb rögzülésére ad módot.
A programmal olyan szerkesztések is készültek, amelyek gyakorlati alkalmazásokat
mutatnak be, mint például a Pulfrich-refraktométer, a változtatható törőszögű
optikai ék, látáshibák korrekciója lencsékkel.
A dolgozatnak a geometriai optika elméleti hátterét tárgyaló fejezetébe beágyazott
ábrák túlnyomó többsége KSEG-ben elkészített dinamikus szerkesztés.
Az elkészült alkalmazások többsége nem került a dolgozatba, a cél minden elkészített
szerkesztésnek összefoglalása és egy honlapon letölthető formában való közzététele.
Formai kritériumok
A grafikai objektumok tetszőleges színben megjeleníthetők.
A pontok megjelenítésére három stílus kínálkozik. A vonalak formázásához három
méret és három stílus (folytonos, pontozott, szaggatott) adott.
A címkék betűtípusa, mérete beállítható, színe az objektum színével megegyező.
A címkék együtt mozognak az objektummal, mozgathatóak az objektum körül, lehetőséget
adva a megfelelő elhelyezésre, fedések elkerülésére.
Az áttekinthetőség érdekében elrejthetjük a segédszerkesztéseket, illetve felfedhetjük
őket.
Előnyök
- Programozási ismereteket nem feltételez.
- A szerkesztések menete könnyen elsajátítható, a transzformációkkal leszármaztatott
objektumaink dinamikusan, reálidőben követik a szülő objektum változásait.
- Kellően átgondolt szerkesztések makrózásával gyorsan és hatékonyan végezhetünk
nagyon bonyolult szerkesztéseket. Példa erre a Weierstrass-szerkesztés.
- A mértani szerkesztéseket kiválóan, gyorsan lehet megejteni.
- Az elkészített szerkesztés több formátumban is elmenthető, lehetőséget
ad különböző képi formátumokban való exportálásra más alkalmazások számára.
- Egyszerűbb mennyiségi összefüggések feltárására alkalmas. A mennyiségi
összefüggések pontosak, Mathcadban számított értékeknek megfelelők.
- A program használata dokumentálódásra késztet, például, ahhoz hogy egy
kúpszelet egy pontjához érintőt húzzunk, ismernünk kell a kúpszeletet generáló
eljárást.
- A kreativitást, képi gondolkodást erősen fejleszti. Tanár, diák egyaránt
felfedezőnek érezheti magát használata közben.
- A geometriai optikában levő jelenségek, képalkotások modelljei pontosan
elkészíthetők. Fény derül a megközelítések mértékére a kapott képhibák alapján.
- Elméleti ismereteket dinamikus képekhez köthetünk. Megérthetjük például
a szem akkomodációját, fényerő szabályozó mechanizmusát, látáshibák korrekcióját,
stb.
Hátrányok
- Nincs lehetőség megjeleníthető – elrejthető
rétegeken dolgozni így megnehezedik, vagy szinte lehetetlenné
válik visszanyomozni a szerkesztés menetét. Egy mentést
követően nem térhetünk vissza a szerkesztésünk
kezdeti fázisaihoz.
- Animáció készítésre nincs lehetőség.
- Egy objektum helyzetének, méreteinek külső megadása nem engedélyezett.
Csak egérrel mozgathatók az objektumok.
- A pontok címkézésében alsó- és felső indexek használata nem lehetséges.
Ez utóbbi oly módon kerülhető meg, hogy helyette címkézzük az őt tartalmazó
görbét és a megfelelő helyre visszük.
- Szövegdoboz nincs, a szöveg csak címke formájában jeleníthető meg.
- Minden mérési adat képernyő pixelben adott. Emiatt célszerű egy elemi
szakasz hosszát mértékegységül venni, így ha vele végig osztjuk mérési eredményeinket
hozzá fogható relatív mennyiségeket kapunk.
- Egérrel való mozgatással tetszőleges pontosságú mérési eredmény nem állítható
be, csak megközelíthető.
- A pontosság növekszik, ha kinagyítjuk a munkafelület azon részét, ahol
a változástatásunk a kívánt eredményhez vezethet.
IV. SZOFTVEREK A FIZIKAOKTATÁSBAN
A fizikaoktatásban a számítógép főbb feladatkörei
a tényanyaggyűjtés (dokumentálódás), illetve az adatfeldolgozás. A digitálisan
elérhető tartalmak a tényanyaggyűjtés, adatfeldolgozás idejét lényegesen lerövidítik.
Az oktatószoftverek dokumentálódást, adatfeldolgozást és tudásszint felmérést
is biztosíthatnak. Számítógépes tényanyaggyűjtésre az internetes keresőmotorok
(Google, Yahoo, AltaVista) a legalkalmasabbak. Az elektronikus formában megjelenő
publikációk gyakran megelőzik a nyomtatásban megjelenő tartalmakat. Az elektronikus
könyvtárakból szabadon letölthető elektronikus könyvek (e-book), a file-megosztással
hozzáférhetővé tett források kimeríthetetlen mennyiségű könyvészetet kínálnak.
Az internet keresőmotorjai ezrével hozzák le a keresőkérdéseknek megfelelő találatokat.
Az angol nyelvű fizika könyvészet messzemenően meghaladja az egyéb nyelveken
publikáltakat, így az angolt kellőképpen nem ismerők lépéshátrányba kerülhetnek.
Az előző fejezetben bemutatott szimulációs szoftver
a KSEG, mellett sok más program is felhasználható. A KSEG
hiányosságai ezekkel a programokkal való összehasonlításból
adódtak. Igényesebb, de fizetős vektorgrafikai alkalmazások
a Geometer’s Sketchpad, valamint a magyar fejlesztésű EUKLIDES.
Utóbbinak van szabadon felhasználható régi verziója,
újabb verziói viszont fizetésesek.
9. EUKLIDES
Az Euklides
program előnyei a KSEG-hez képest az alábbiak:
- négyzethálós munkafelület vonalzókkal, a rácsállandónak három lehetséges
értékét lehet cm-ben beállítani;
- több réteges munkalehetőség, ki-be kapcsolható láthatósággal;
- helyzetek és méretek kiírása a rácsállandó beállításnak megfelelő,
- a
bázispont ugorhat objektumhoz, rácsponthoz,
- több beépített szerkesztés:
nyilak, érintők, kúpszeletek, transzformációk,
- animálási lehetőség,
animáció kétirányú lejátszása automatikusan vagy lépésekben;
Hátrányai a KSEG-hez képest:
- a bázispontok lebegnek, csak ideiglenesen köthetők adott objektumhoz
- a bázispont mozgatásával a kényszerfeltételek, görbéhez kötöttség megszűnik
és értelmezhetetlenné teszi a szerkesztést
- animációra orientáltsága nem jelenti a lényeg legszemléletesebb megragadását.
Sok előnye és kevés hátránya mellett nem rá esett a választásom,
mert az animáció helyettesíthető a bázispontok tetszés szerinti mozgatásával
a kényszerítő feltételek megmaradása mellett.
A vektorgrafikai programokat nem számítási feladatok szimulációjára dolgozták
ki. Amennyiben sok adat feldolgozását, függvénykapcsolatainak elemzését szeretnénk
elvégezni, erre megfelelő lehet a Microsoft Office termékcsalád Excel programja.
10. EXCEL
Számítógépes adatfeldolgozásra is sok szoftver íródott. A Microsoft
Office alkalmazásai közül az Excel hatalmas adatmennyiség kezelésére, feldolgozására
alkalmas. Beépített függvényei számos adatfeldolgozási stratégiát tesznek lehetővé.
Az adatok különböző táblázatokba szervezhetők, adatokra épülő kimutatás-diagramokat
készíthetünk, függvényeket ábrázolhatunk. Tehetjük mindezt programozási ismeretek
hiányában is.
Az alábbi diagram (33. ábra)
szemlélteti a programban rejlő matematikai képességeket.
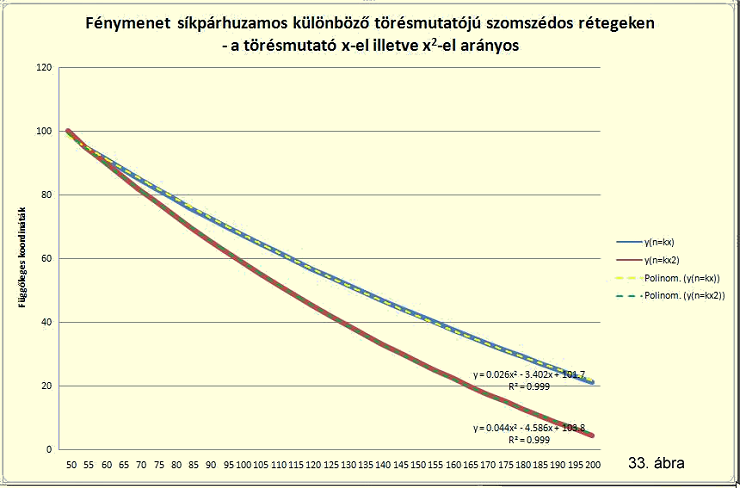
(Excel
file letöltése itt)
A diagram fénymenetet ábrázol, amint egy optikai közeg
N darab szomszédos függőleges állású
síkpárhuzamos lemezén halad. Változtatható
paraméterekként a beesési szöget és a lemezvastagságot
adtam meg. A síkpárhuzamos lemezek törésmutatója
az x koordinátával egyenesen arányos a kék vonal
esetében és x2-tel a piros vonal esetében. A
grafikonon egy-egy másodrendű polinomiális közelítésű
trendvonal is fel lett véve, a megfelelő grafikonokon fel lettek
tüntetve a közelítő függvények polinomiális
együtthatóikkal. A grafikonok a kezdeti feltételek módosításával
együtt változnak. Minél több pontpárt tüntetünk
fel, annál magasabb fokú polinomiális megközelítésű
trendvonal illeszkedik hozzá. Az Excel legpontosabb trendvonalát
hatodfokú polinom adja. R2 –a legkisebb négyzetes
eltérést jellemzi, minél jobban közelít egyhez,
annál pontosabb az illeszkedés. Amennyiben a szomszédos
síkpárhuzamos lemezek közötti törésmutató-eltérés
kicsi és a fény egyre nagyobb törésmutatójú
lemezek fele halad aszimptotikusan közeledik az utolsó lemez beesési
merőlegeséhez.
11. CROCODILE PHYSICS
A Crocodile
Physics fizikára írt, fizetős, szimulációs szoftver. A Crocodile Physics
egy nagyobb csomag része, a fejlesztői csoport kidolgozott matematika, technológia,
kémia és informatika szoftvert is. A fizika rész az alábbi fejezetekre van osztva:
- mozgás
- erő és gyorsulás
- mozgás és energia
- áramkörök
- elektromos energia
- hullámok
- optika
Az optika rész felépítése a következő:
- Előre elkészített funkcionális modellek
- Részmodellek
Az előre elkészített szimulációk között
megtalálhatók a fényvisszaverődés, fénytörés, sík- és gömbtükrök, lencsék, nagyítás,
nagyítók (lupék), fényképezőgép, periszkóp, teleszkóp és ezenkívül több mint
35 alkalmazás.
A részmodelleknél az alábbiakat találjuk: optikai tér, sugárdiagramok (közeli
tárgy, távoli tárgy, szem, ernyő), fényforrások (széttartó nyaláb, párhuzamos
nyaláb, lézerdoboz), lencsék (konvex, konkáv), tükrök (sík, gömb (konvex, konkáv),
parabolikus), átlátszó tárgy (prizma főmetszete, téglalap, félkör), átlátszatlan
tárgy (állítható rés, téglalap, körlap, háromszög), mérőeszközök (távolság jelölő,
vonalzó, szögmérő).
A program lehetőséget nyújt a részmodellek funkcionális modellé szervezésére.
A részmodellek igény szerinti összeillesztésével készíthetők az új modellek,
szimulációk. A modellalkotás a lego-játékhoz hasonló. A részekhez paraméterlisták
tartóznak, amelyeken keresztül a rész minden lényeges tulajdonsága beállítható,
numerikusan megadott értékek vagy begördülő választó listákból való kijelölés
alapján. A különböző tulajdonságok változtatását megengedhetjük vagy tilthatjuk.
Zárolhatunk helyzetet, méretet, irányítást, tulajdonság szerkesztést. A paraméterek
közül a numerikusan beállíthatóakat és a választó listásakat a munkafelületre
elhelyezhető vezérlőkkel is állíthatjuk a tulajdonság-panel nyújtotta lehetőség
mellett.
Az új modell létrehozásának a menetének ismertetéséhez létrehozzuk a rövidlátás
javítólencsével való korrekcióját bemutató szimulációt (34.
ábra).
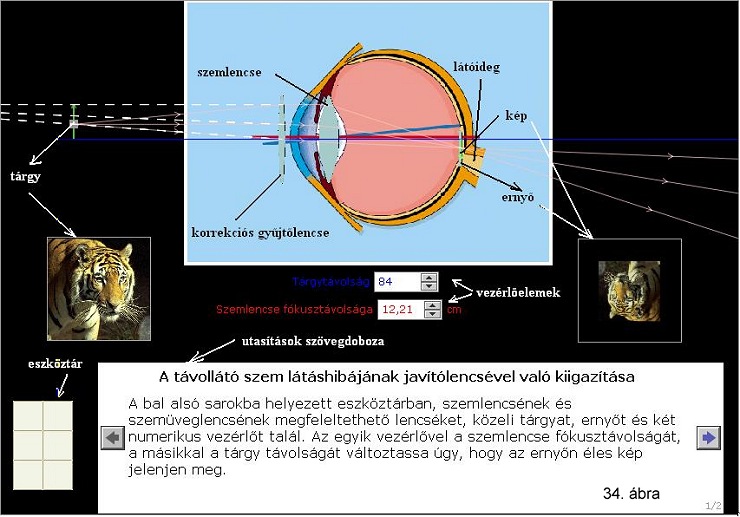
A modell az alábbi részekből épült fel:
- optikai tér
- szemet ábrázoló kép
- két darab konvex lencse
- közeli tárgy
- ernyő
- két numerikus vezérlőelem
- utasításokat tartalmazó szövegdoboz
- eszköztár: részmodelleket ideiglenesen raktározó (2x3-as) mező.
A modell egy részét előre elkészítjük, a többit a felhasználónak
kell összerakni az utasításaink alapján. Először a munkafelületre egérrel behúzzuk
az optikai teret jelentő keretet. Elhelyezzük benne a szem illusztrációját,
ez egy korábban elmentett kép-file, majd letiltjuk a tulajdonságainak szerkesztési
lehetőségét. Elhelyezzük az optikai térben az utasításokat tartalmazó szövegdobozt
és az üres eszköztárat, utóbbit feltöltjük a többi részmodellel. Ezzel lehetőséget
kínálunk a felhasználónak a modell sajátkezű összerakására. A modellalkotás
első fejezete elkészült.
A második részben utasításainknak megfelelően építi tovább a modellt a felhasználó.
Az eszköztárból az optikai térbe a megfelelő helyekre kerülnek a részek. A két
numerikus vezérlőelemmel változtatható a közeli tárgy helyzete, illetve a szemlencsét
jelképező lencse fókusztávolsága. A retina-látóideg csatlakozási helyére elhelyezett
ernyőn megjelenik a tárgy valódi képe. A tárgytávolság és a szemlencse fókusztávolságának
változtatásával nem sikerül éles képet létrehozni mindaddig, amíg korrekciós
gyűjtőlencsénket nem tesszük közvetlen a szem elé. Ezt követően sikerül az éleslátást
beállítani, ami az ernyőhöz csatolt kép minősége alapján szembetűnő.
A közeli tárgynál beállítható, hogy melyik pontjából, hány fénysugár induljon
ki. Választhatunk mozgópont, talppont és csúcspont közül (akár az összes pontot
egyidejűleg kiválaszthatjuk). A tárgyat jelentő képek egy begördülő listából
választhatók (itt tigris lett kiválasztva). A tárgynál bejelölhető az optikai
eszközök közbenső képének megfelelő sugármenet (szaggatott fehér vonalak utalnak
a javító lencse által létrehozott képre, itt nem látszik a közbenső kép, mert
az ábrán kívülre esik).
A szimuláció alapján az alábbi következtetések vonhatók le:
- a tárgy közeledésekor a szemlencse törőképességének növekedni kell az éleslátáshoz,
ez a szemlencse görbületi sugarának csökkentésével jár,
- a rövidlátó szem látáshibáját úgy javítja a korrekciós lencse, hogy a közeli
tárgyról virtuális, egyenes állású, nagyított és távolba vitt közbenső képet
alkot, a szem tehát végül ezt a közbenső képet képezi le.
A program nyújtotta lehetőségek bőségesen megfelelnek a geometriai fénytan jelenségeinek
modellezésére, mindazonáltal aki magasabb szintű, átfogóbb modelleket szeretne
és a programozás nem idegen számára az java programozási nyelvben megírhatja
a modelleket. A java objektum orientált lényege, lehetővé teszi a már elkészült
(mások által elkészített) objektumok beépítését, felgyorsítva ezáltal a modell
megalkotását. A NETBEANS program nagy segítségére lehet a java programozónak.
Kidolgozója a Sun Microsystems és teljesen ingyenesen letölthető és korlátozás
nélkül használható. A java nyelvet jól ismerőknek a honlapokba ágyazható applet-ek
a legalkalmasabbak a szimulációk készítésére.
12. APPLET
Az applet HTML dokumentumokba beágyazható, Java programnyelven
megírt alkalmazás. Segítségükkel az internet honlapjai biztosítani tudják a
felhasználó számára az interaktivitást. Az interneten rengeteg fizika oktatást-népszerűsítést
tartalmazó applet található. Előnyük abból származik, hogy nincs szükség külön
szoftverre a lejátszásukhoz. A böngészők túlnyomó többségébe be lett ágyazva
a Java kódok fordítója, a Java Virtual Machine. A hátrányhoz sorolható, hogy
a forráskód közzététele hiányában még a programozó sem tudja a modellt módosítani,
nem beszélve arról, hogy az átlagos felhasználónak nincsenek programozási ismeretei.
Megfelelő programozási- és fizika ismeretek birtokában a java programozó bármilyen
szimulációs feladatot képes kidolgozni.
Az alábbi applet egy vékony gyűjtőlencse képalkotását
bemutató applet segítségével készült. A szimulációban változtathatjuk a lencse
fókusztávolságát valamint a tárgy vonalas méretét és helyzetét. Az applet kiírja
az aktuális fókusz-, tárgy- és képtávolságokat. A képalkotás torzításmentes
megközelítésében a mélységbeli nagyítás a vonalas nagyítással egyenlő. Az applet
forráskódja a függelékben található.
A fenti applet egy gyűjtőlencse képalkotását szemlélteti. A
tárgyat és képet egy-egy kék téglalap jelöli. Az egérrel változtatható a lencse
fókusztávolsága az F1 tárgytéri fókuszpont mozgatásával. A tárgytávolság
és méret a tárgy tetejének húzásával érhető el. Az applet kiírja az aktuális
tárgy-, kép- és fókusztávolságot.
13. MATHCAD
A Mathcad
egy matematikai szoftver. A program képességei nagyon széleskörűek, alapszintű
felhasználása nem igényel programozási ismereteket. Vektoralgebrától matematikai
analízisig mindent felölel. Egy tetszőleges függvény esetében, pillanatok alatt
kiszámítja a gyökeit, deriváltjait, integráljait, határértékeit, faktorizál,
Taylor-sorba fejt. A függvényábrázoláshoz csak az értelmezési tartományt kell
megadni.
A dolgozatban, a KSEG-ben adódó bonyolultabb matematikai összefüggések helyességét
segítségével ellenőriztem, például a prizma eltérítési szögére KSEG-ben és Mathcadban
is ugyanaz a megoldás adódott. Animációkat is készíthetünk Mathcadban. Ehhez
az szükséges, hogy egy értelmezési tartományban egy úgynevezett FRAME változót
iktassunk. A FRAME változón keresztül egy függvény paraméterezhető és ennek
a paraméternek megfelelően változik a grafikus képe.
A gyűjtőlencse képtávolságának illetve vonalas nagyításának változása a tárgytávolság
függvényében letölthető
avi fájlban. Megfigyelhető, hogy a fókusztávolságban mindkét függvény "elszakad",
nem folytonos hiszen ott nincs kép.
Az alábbi Mathcadban készült animáció (36. ábra)
egy szinuszosan változó törésmutatójú szomszédos síkpárhuzamos lemezeken áthaladó
fényutat szemléltet. A tömböt N darab síkpárhuzamos lemezre bontottam, a törésmutató
lemezenként állandó, két szomszédos lemezé különböző. A törésmutató 2+sin(x)
függvényként értelmezett a példában.
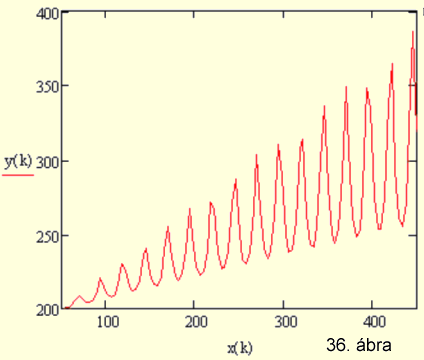
A szimulációról avi
videoklip készült.
V. KÖVETKEZTETÉSEK
Az utóbbi években, hazánkban a természettudományok oktatása
háttérbe szorult, afféle mostohagyermekké vált. A rendszerváltást követően,
az ipar hanyatlása következtében egyre kevesebb mérnökre lett szükség. A határok
megnyitása, az Európai Unióba való csatlakozás, felértékelte az idegennyelv-ismeretet,
talán kissé a természettudományok rovására. A piaci követelmények nem igényeltek
sok természettudományos végzettségű munkaerőt.
Azok, akik tudásukkal, tanulmányaikkal, ezekből származó találmányaikkal lényegében
mindenkinek az életminőségét javították, a törvényhozásban alul képviseltek,
véleményformáló szavaik csak ritkán kerülnek a köztudatba.
Mindemellett mára ez a tendencia megfordulni látszik. A multinacionális cégek
letelepedésével, az építőipar, személygépkocsi gyártás dinamikus fejlődésével
egyre keresettebbé válnak a mérnökök. Az oktatási rendszerre hárul a felelősség,
hogy jól képzett szakembereket adjon a társadalomnak. Azon megfontolás alapján,
hogy egy termék ára leginkább a legyártásához szükséges tudásbázis függvénye,
jogosnak tűnik több figyelmet fordítani a természettudományoknak, illetve a
természettudományos tartalmak hatékonyabb feldolgozásának.
Dolgozatom a fizika aktív módszereinek a skáláját szeretné népszerűsíteni és
kissé kibővíteni. A nagy számok törvénye alapján, minél többen tapasztalják
meg a természeti törvények egyszerűségét, szépségét, annál többen fogják alkotó
erejüket, kreativitásukat e téren kamatoztatni, illetve szavukat hallatni fizikai
környezetünk globális problémáinak megoldásában. A számítógépes szimulációk
segítenek felfedni a nehezebben hozzáférhető, észlelhető tartalmakat és a felhasználó
számára aktív beavatkozási lehetőséget kínálnak.
A vektorgrafikus megoldású szimulációk legfőbb hozadéka, hogy segítségükkel
tanár, diák egyaránt, programozási ismeretek hiányában is, feldolgozhatja a
geometriai fénytant líceumi szintig. Teheti mindezt úgy, hogy letölti a meglévő
modelleket vagy maga készíti el őket, otthon, laboratóriumban vagy akár szünetben
egy iskolai számítógépen. A modellezés folyamatában ráébredhetünk, mennyire
alaposak ismereteink a geometriai fénytan területén, mennyire jók azok a modellek,
amelyek immár az agyunkba, gondolkodásunkba beépültek. Az adódó problémák megoldásával
az alaposabb tudás ágyát vethetjük meg, így aztán az ily módon rögzült információk
sokkal érdekesebb alkalmazásokban fejezhetők ki. Az érdekessé tett tartalmak
pedig a fizika népszerűségét növelik.
Könyvészet
1. Angster, E. 2002. Objektumorientált tervezés és programozás. Martonvásár.
Akadémiai Nyomda.
2. Barter, J. 2005. Telescopes. The Lucent Library of Science and Technology.
Farmington Hills. Thomson Gale.
3. Born, Max. 1986. Principles of Optics. Exeter. Wheaton & Co.
Ltd.
4. Cutnell, J.D., Johnson, W. J. 2007. Physics, 7th Edition. Wiley,
John & Sons, Incorporated.
5. Fhisbane, P., Gasiorowtz, S., Thornton, S. 2005. Physics for scientists
and engineers with modern physics. New Jersey. Pearson Educational International.
Pearson Prentice Hall.
6. Greene, D. 2003. Light and Dark. Bristol. IOP Publishing Ltd.
7. Halliday. Resnick. Walker. 2007. Fundamentals of Physics. Wiley,
John & Sons, Incorporated.
8. Johnson, B. K. 1960. Optics and Optical Instruments. New York. Dover
Publications, Inc.
9. Kovács Kálmán. 1985 . A fény elméletben és gyakorlatban. Kolozsvár.
Dacia Könyvkiadó.
10. Kovács Zoltán. 1994. A fizikatanítás módszertana. Kolozsvár. UBB
Cluj.
11. Simonyi Károly. 1998. A fizika kultúrtörténete. Budapest. Akadémiai
Kiadó.
12. Şteţiu, P. 1979. Fizică (capitolul Optică). Cluj-Napoca. UBB Cluj.
(egyetemi jegyzet).
Internetes források - honlapok, Java alkalmazások
A
fizika éve
Celebrate.digitalbrain.com
Celebrate.digitalbrain.com
(magyarul is)
Didactic.ro-Fizica
- lectii, manuale, planificare, planificari, teste, lectie
Java alkalmazások
a fizika tanításához (Java 1.4)
JAVA Index
PhET
-Fizika- Simulations
Physics in
Hungary
Physlet
Resource CD
SuliFizika-ELTE
Teszt
- fényjelenségek
Fizika.lap.hu
Fizikai Szemle
Fizika
Kísérletek Gyűjtemény I.
Howstuffworks
Physical Science Channel
Math, Physics,
and Engineering Applets
Physics
and Flash
Science Toys
Smile Program
Physics Index
The
Nobel Prize in Physics—Educational
The Physics Classroom
Letöltések
KSEG-fájlok
egy csomagban. A KSEG fájlok hiperlinkes letöltési ablakaiban a megnyitás
helyett a mentés opciót válasszuk. A mentett fájlokat a KSEG programból lehet
csak megnyitni. Amennyiben semmit nem lát a megnyitást követően, kattintson
a kétirányú nagyítóeszköz képikonjára, ezzel az egész szerkesztés a látómezőbe
skálázódik. Lásd az alábbi ábrán. A szerkesztésekhez felhasznált makrókat töltse
le innen.

Függelék
Vékony gyűjtőlencse képalkotásának
java nyelvű forráskódja
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
public class Gyujtolencse extends JApplet
implements MouseListener, MouseMotionListener {
int xF1, yF; // tárgytéri fókusz koordinátái
int xF2; // képtéri fókusz helyzete
int xT, yT; // tárgycsúcs helyzete.
int xL, yL; //lencse középpontja
/* egérrel való mozgatás paraméterei */
boolean dragging; // igaz, ha folyamatban van a vontatás.
boolean dragRedSquare;
int offsetX, offsetY; // egérmutató koordinátái
// tárgycsúcsra kattintás esetén
JPanel drawSurface; // a tényleges rajzvászon
// az applet tartalom panellje
public void init() {
// inicializálja az appletet a mozgatható kezdeti értékek
// beállításával és létrehozza a rajzolási felületet,
// majd telepíti az applet gyűjtőpaneljeként
xF1 = 60; // fókuszpont helyzete
yF = 80;
xT = 50; //tárgy-csúcs koord
yT = 75;
drawSurface = new JPanel() {
// rajzolási munkaterület létrehozása az applet számára
public void paintComponent(Graphics g) {
super.paintComponent(g); // Háttérszínnel kitölt.
xL=getWidth()/2; //a lencse x,y-helyzete
yL=getHeight()/4;
xF2=xL+xL-xF1;
yF=getHeight()/2;
if (xT==xF1){xT=xT+1;}
int xK = xL+(xL-xT)*(xL-xF1)/(xF1-xT); //kep x-koordinata
int yK = yF+(yF-yT)*(xK-xL)/(xL-xT); //kep y-koordinata
g.drawOval(xL,yL,6, 2*yL);
g.drawString("Gyűjtő lencse",xL-35,yL-2);
g.drawString("A tárgytávolság: xt = "+(xL-xT)+" cm",30,2*yF-100);
g.drawString("A fókusztávolság: f = "+(xF2-xL)+" cm",30,2*yF-60);
if(Math.abs(xT-xF1)<5){
g.setColor(Color.RED);
g.drawString("A kép a végtelenben keletkezik, ha xt=f!",30,yF+40);
g.setColor(Color.BLACK);
}
if(xT<xF1){
g.drawString("A képtávolság: xk = "+(-1)*(xL-xK)+" cm",30,2*yF-80);
}
else {
g.drawString("A képtávolság: xk = "+(xK-xL)+" cm",30,2*yF-80);
}
g.drawString("A",xT-2,yF+20);
g.drawString("B",xT-2,yT-5);
g.fillOval(xK-2, yF-2, 6, 6); //kép talpa
if (xK<=xL){
g.drawString("A'",xK-2,yF+20);
g.drawString("B'",xK-2,yK-5);}
else{
g.drawString("A'",xK-2,yF-5);
g.drawString("B'",xK-2,yK+20);
}
g.fillOval(xK-2, yK-2, 6, 6); //kép csúcsa
// y2=getHeight()/2-30;
g.drawLine(0,getHeight()/2,getWidth(),getHeight()/2);
g.setColor(Color.red);
g.fillOval(xF1-2, yF-2, 6, 6); //tárgytéri fókuszpont
g.drawString("F1",xF1-2,yF-5);
g.fillOval(xF2-2, yF-2, 6, 6); //képtéri fókuszpont
g.drawString("F2",xF2-2,yF-5);
g.setColor(Color.cyan);
g.fillOval(xL,yL,6, 2*yL); //lencse
g.setColor(Color.blue);
g.fillRect(xT, yT, 10, getHeight()/2-yT); //tárgy
if(xK>=xL)
g.fillRect(xK, yF, 10*(xK-xL)/(xL-xT), yK-yF);
if(xK<=xL)//kep
g.fillRect(xK, yK, -10*(xK-xL)/(xL-xT), -(yK-yF));
g.drawLine(xK,yK,xK,yF); //kép vonala
g.setColor(Color.yellow);
g.drawLine(xT,yT,xL,yT);//opt.tg.-el párhuzamos
//g.fillRect(xT, getHeight()/2, 10, yT-getHeight()/2);//
g.drawRect(0,0,getSize().width-1,getSize().height-1);//belső szegély
g.drawLine(xL,yT,xF2,yF); //képtéri fókuszig tartó szakasz
g.drawLine(xF2,yF,xF2+30*(xF2-xL),yF+30*(yF-yT)); //az F2-n átmenő meghosszabbított
X30 sugár
g.drawLine(xT,yT,xL,yF); //tárgycsúcsból lencseközépig
g.drawLine(xL,yF,xL+30*(xL-xT),yF+30*(yF-yT)); //a lencse közepén meghosszabbított
X30
g.drawLine(xK,yK,xT,yT); //virtuális tárgycsúcs-képcsúcs
g.drawLine(xK,yK,xL,yT); // virtuális képcsúcs-párhuzamos-vég
}
};
drawSurface.setBackground(Color.white);
drawSurface.addMouseListener(this);
drawSurface.addMouseMotionListener(this);
setContentPane(drawSurface);
} // end init();
public void mousePressed(MouseEvent evt) {
// lenyomva tartott egérgombra reagál.
// ellenőrzi, hogy érzékeny terület fölött van
//ha igen, vontatni lehet.
if (dragging) //kilép, ha már van egérvontatási esemény.
return;
int x = evt.getX(); // kattintás helye.
int y = evt.getY();
if (x >= xT && x < xT+10 && y >= yT-5 && y
< yT+5) {
//tetejétől mozgatható a tárgyat jelölő téglalap
dragging = true;
dragRedSquare = false;
offsetX = x - xT;
}
else if (x >= xF1 && x < xF1+10 && y >= yF &&
y < yF+10) {
// akkor a fókuszpont helyzete változtatatható.
dragging = true;
dragRedSquare = true;
offsetX = x - xF1;
offsetY = y - yF;
}
}
public void mouseReleased(MouseEvent evt) {
// egérgomb felengedésre vontatást abbahagy.
dragging = false;
}
public void mouseDragged(MouseEvent evt) {
// Egérhúzásra aktiválódik. Ha nincs az érzékenységi
// zóna fölött, akkor kilép, ellenkező esetben változtatja a helyzet koordinátáit.
if (dragging == false)
return;
int x = evt.getX();
int y = evt.getY();
if (dragRedSquare) { // Fókuszpont mozgatása.
if(x>2 && x<=getSize().width/2-2)
xF1 = x ;//- offsetX;
}
else { // tárgypontot mozgat.
if(x>2 && x<=getSize().width/2-2)
xT = x ;//- offsetX;
if(y<=getSize().height/2 && y>=yL)
yT = y ;//- offsetY;
}
drawSurface.repaint();
}
public void mouseMoved(MouseEvent evt) { }
public void mouseClicked(MouseEvent evt) { }
public void mouseEntered(MouseEvent evt) { }
public void mouseExited(MouseEvent evt) { }
public static void main(String args[]) {
JFrame f = new JFrame("Lencse képalkotása"); //keretet ad hozza, hogy
onalloan megjelenjen
Gyujtolencse dTS = new Gyujtolencse();
dTS.init();
dTS.start();
f.add("Center", dTS);
f.setSize(500, 400);
f.show();
}
}
 Az első pontos méréseket, földi tárgyakat igénybe véve, Fizeau
végzi 1849-ben. A méréshez négy lencsét, két síktükröt (az egyik féligáteresztő) és egy fogaskereket használt. A baloldali tükör a fényutat megduplázza (16 km),
a lencsék párhuzamosítják a nyalábot illetve fokalizálják két fog közötti hézagra.
A féligáteresztő tükrön és a párhuzamosító okulárlencsén keresztül szemlélik
a távoli tükörről visszaverődő nyalábot. A fogaskerék sebességét addig növelik,
amíg a visszaverődő nyaláb nem jut a szembe, mert elárnyékolja az elébe kerülő
fog. Ezt a forgási sebességet a duplájára növelve, lesz a legnagyobb a szembe
jutó fényáram, mert a következő hézagon keresztül a visszavert nyaláb egészében
eljut a megfigyelő szemébe. E módszerrel a fény sebességére kapott érték 315
000 km/s volt.
Az első pontos méréseket, földi tárgyakat igénybe véve, Fizeau
végzi 1849-ben. A méréshez négy lencsét, két síktükröt (az egyik féligáteresztő) és egy fogaskereket használt. A baloldali tükör a fényutat megduplázza (16 km),
a lencsék párhuzamosítják a nyalábot illetve fokalizálják két fog közötti hézagra.
A féligáteresztő tükrön és a párhuzamosító okulárlencsén keresztül szemlélik
a távoli tükörről visszaverődő nyalábot. A fogaskerék sebességét addig növelik,
amíg a visszaverődő nyaláb nem jut a szembe, mert elárnyékolja az elébe kerülő
fog. Ezt a forgási sebességet a duplájára növelve, lesz a legnagyobb a szembe
jutó fényáram, mert a következő hézagon keresztül a visszavert nyaláb egészében
eljut a megfigyelő szemébe. E módszerrel a fény sebességére kapott érték 315
000 km/s volt.
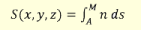 (2.2)
(2.2)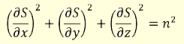 (2.3)
(2.3)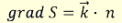 (2.4)
(2.4)

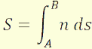
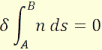 (2.5)
(2.5)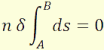
 Fényvisszaverődésnek nevezzük azt a fényjelenséget mikor két
optikai közeget elválasztó határfelületre eső fény visszatér abba a közegbe,
ahonnan érkezett.
Fényvisszaverődésnek nevezzük azt a fényjelenséget mikor két
optikai közeget elválasztó határfelületre eső fény visszatér abba a közegbe,
ahonnan érkezett.
 A síktükör az A pontból feléje tartó sugarat a B ponton keresztül
veri vissza. Feltételezzük, hogy a fénysugár az I pontból verődik vissza. Meghatározzuk
az I beesési pont helyzetét úgy, hogy az AIB utat a fény a legrövidebb idő alatt
tegye meg. Ehhez meghatározzuk y értékét. Adottnak tekinthetők a h1, h2 tükörig
mért távolságok, valamint az A és B pontok tükörre eső vetületeinek a w távolsága.
A síktükör az A pontból feléje tartó sugarat a B ponton keresztül
veri vissza. Feltételezzük, hogy a fénysugár az I pontból verődik vissza. Meghatározzuk
az I beesési pont helyzetét úgy, hogy az AIB utat a fény a legrövidebb idő alatt
tegye meg. Ehhez meghatározzuk y értékét. Adottnak tekinthetők a h1, h2 tükörig
mért távolságok, valamint az A és B pontok tükörre eső vetületeinek a w távolsága.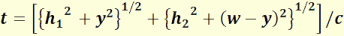 (2.6)
(2.6)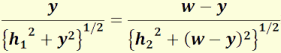 (2.7)
(2.7) Annak az igazolására, hogy a beesési merőleges, a beeső- és a visszavert fénysugár
egy síkban van, tekintsük a 6. ábrát.
Annak az igazolására, hogy a beesési merőleges, a beeső- és a visszavert fénysugár
egy síkban van, tekintsük a 6. ábrát.
 A
szürkével jelölt sűrűbb optikai közeg A pontjából a jobboldali, ritkább optikai
közeg B pontjába érkezik a fénysugár. Tudva, hogy a közegek homogének és bennük
egyenes mentén terjed a fény, a feladat az I beesési pont helyzetének a meghatározására
korlátozódik, ezt az y változóval jellemezzük. A vákuumban való terjedéshez
képest a két közegben a terjedési idő n1 illetve n2-ször
nagyobb.
A
szürkével jelölt sűrűbb optikai közeg A pontjából a jobboldali, ritkább optikai
közeg B pontjába érkezik a fénysugár. Tudva, hogy a közegek homogének és bennük
egyenes mentén terjed a fény, a feladat az I beesési pont helyzetének a meghatározására
korlátozódik, ezt az y változóval jellemezzük. A vákuumban való terjedéshez
képest a két közegben a terjedési idő n1 illetve n2-ször
nagyobb.  (2.9)
(2.9)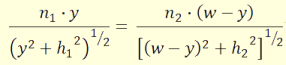 (2.10)
(2.10) Mivel a szögek egyaránt nőnek vagy csökkennek (de nem arányosan),
emiatt i > L –re nincs valós megoldás, mert r
nem lehet 90 foknál nagyobb. Valóban L-nél
nagyobb értékekre nincs fénytörés, a fellépő jelenség a teljes fényvisszaverődés.
A jelenség szemléltetése a 8. ábrán
Mivel a szögek egyaránt nőnek vagy csökkennek (de nem arányosan),
emiatt i > L –re nincs valós megoldás, mert r
nem lehet 90 foknál nagyobb. Valóban L-nél
nagyobb értékekre nincs fénytörés, a fellépő jelenség a teljes fényvisszaverődés.
A jelenség szemléltetése a 8. ábrán 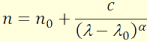 (2.15)
(2.15) Az n0, c, λ0 és α0 empirikus állandókat
négy hullámhosszra megmért törésmutató értékekből határozzák meg [9]. α
értéke körülbelül 1.2, de 1-re is elég pontos
a közelítés és elegendő három hullámhosszra
elvégezni a méréseket. A 9. ábra
egy anyag diszperzió függvényét szemlélteti
a 400 – 700 nm-es tartományban.
Az n0, c, λ0 és α0 empirikus állandókat
négy hullámhosszra megmért törésmutató értékekből határozzák meg [9]. α
értéke körülbelül 1.2, de 1-re is elég pontos
a közelítés és elegendő három hullámhosszra
elvégezni a méréseket. A 9. ábra
egy anyag diszperzió függvényét szemlélteti
a 400 – 700 nm-es tartományban.

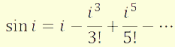
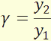 (3.1)
(3.1)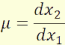 (3.2)
(3.2)

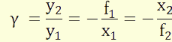 (3.3)
(3.3)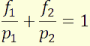 (3.5)
(3.5)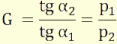 (3.6)
(3.6)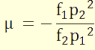 (3.9)
(3.9)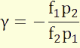 (3.11)
(3.11)
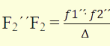 (3.14)
(3.14)
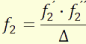 (3.15)
(3.15)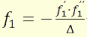 (3.16)
(3.16)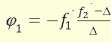 (3.17)
(3.17)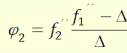 (3.18)
(3.18)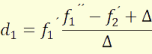 (3.19)
(3.19)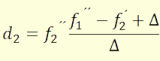 (3.20)
(3.20)

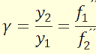 (3.22)
(3.22)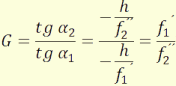 (3.23)
(3.23) (3.24)
(3.24)
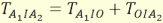 (4.1)
(4.1) 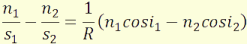 (4.2)
(4.2)

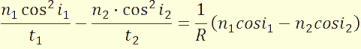 (4.3)
(4.3)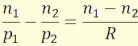 (4.4)
(4.4)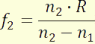 (4.5)
(4.5)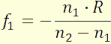 (4.6)
(4.6)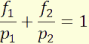 (4.7)
(4.7)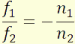 (4.9)
(4.9)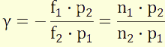 (4.11)
(4.11)
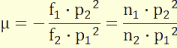 (4.12)
(4.12)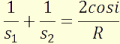 (4.13)
(4.13)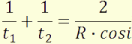 (4.14)
(4.14)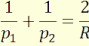 (4.15)
(4.15)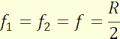 (4.16)
(4.16)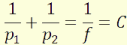 (4.17)
(4.17)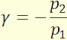 (4.18)
(4.18)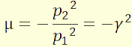 (4.19)
(4.19)


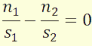 (4.20)
(4.20)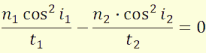 (4.21)
(4.21)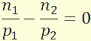 (4.22)
(4.22) A 20. ábrán
A 20. ábrán 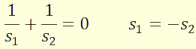 (4.23)
(4.23)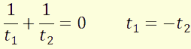 (4.24)
(4.24)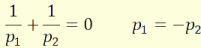 (4.25)
(4.25)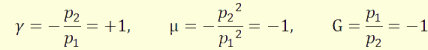 (4.26)
(4.26)


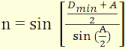 (4.29)
(4.29)
 Nagyobb törőszögűek a tengelytől távolabbi elemi prizmák.
A nagyobb törőszögnek viszont nagyobb eltérítési szög felel meg, ezért a lencse
a csúcsához közeli sugarakat erősebben téríti el.
Nagyobb törőszögűek a tengelytől távolabbi elemi prizmák.
A nagyobb törőszögnek viszont nagyobb eltérítési szög felel meg, ezért a lencse
a csúcsához közeli sugarakat erősebben téríti el. 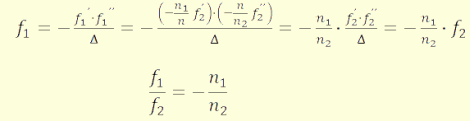 (4.31)
(4.31)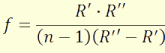 (4.32)
(4.32)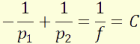 (4.34)
(4.34)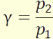 (4.35)
(4.35)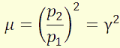 (4.36)
(4.36)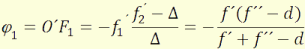 (4.39)
(4.39)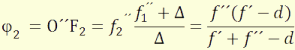 (4.40)
(4.40)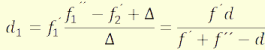 (4.41)
(4.41)
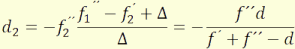 (4.42)
(4.42)




 egyenletrendszert megoldva meghatározható a és b paraméterek értéke.
egyenletrendszert megoldva meghatározható a és b paraméterek értéke. Határozott integrállal egy folytonosan változó függvény által
meghatározott vonalhosszat, területet vagy térfogatot számítunk ki. Ha például
az erő változik az x koordináták szerint, akkor az xA, xB
intervallumon való elmozdulás során végzett munkája az F(x) függvény grafikus
képe és az Ox tengely közé eső területtel egyenlő (a mellékelt ábrán a szürke
terület),
amit az
Határozott integrállal egy folytonosan változó függvény által
meghatározott vonalhosszat, területet vagy térfogatot számítunk ki. Ha például
az erő változik az x koordináták szerint, akkor az xA, xB
intervallumon való elmozdulás során végzett munkája az F(x) függvény grafikus
képe és az Ox tengely közé eső területtel egyenlő (a mellékelt ábrán a szürke
terület),
amit az 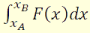 integrállal
számolunk ki.
integrállal
számolunk ki. 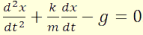 .
A súrlódási erő a sebességgel arányos (k·dx/dt), tehát a csepp gyorsulása
is változik.
.
A súrlódási erő a sebességgel arányos (k·dx/dt), tehát a csepp gyorsulása
is változik. 






