A kutatások kiemelkedő tudományterületei

A matematika számos területén értek el magyar matematikusok figyelemreméltó eredményeket. A következőkben csak a hosszabb ideig művelt jelentősebb témák kerülnek szóba. Az egyes területek kijelölése némiképpen önkényes, mert egy-egy diszciplína több területhez is tartozhat. Hasonló a helyzet az egyes területeken említett tudósokkal is, mert sokan több területen is jelentős eredményeket értek el.

A matematikai analízis kutatásának nagy hagyományai vannak. Fejér Lipót, Haar Alfréd és Riesz Frigyes munkássága a matematikai analízis fejlődésében döntő szerepet játszott. A valós függvénytanban Riesz Frigyes és Császár Ákos, a komplex függvénytanban Dienes Pál, Fekete Mihály, Pólya György, Szász Ottó, Szegő Gábor, Riesz Frigyes, Fejér Lipót és Turán Pál ért el kiemelkedő eredményeket.

Dienes Pál (1882–1952) komplex változós függvényekkel, differenciálgeometriával, végtelen mátrixokkal, matematikai logikával és filozófiai kérdésekkel is foglalkozott. Legjelentősebb eredményeit Taylor-soroknak a konvergencia körükön való viselkedésével kapcsolatban érte el. Több fontos monográfiát írt. Fekete Mihály (1886–1957) főként sorelmélettel és komplex analízissel, Szász vagy Száz Ottó (1884 v. 1899–1952) főként valós analízissel, Fourier-sorokkal foglalkozott.Szegő Gábor (1895-1985) Pólya Györggyel írt nagy hatású közös könyvet: Aufgaben und Lehrsatze aus Analysis, 1–2. (1925, magyarul Feladatok és tételek az analízis köréből, 1980) Legfontosabb kutatásait az extremális problémák és a Töplitz-mátrixok területén végezte. Ulf Grenanderrel együtt írta Toeplitz forms and their applications (1958) c. alapvető munkáját. Az Orthogonal Polynomials (1939) ugyancsak alapmunkának számít.

{IV-37.} A differenciálegyenletek területén a kutatásokat Vályi Gyula, Kürschák József és Schlesinger Lajos kezdte el. Későbbi művelői közül említést kell tenni Erdélyi Artúrról, Egerváry Jenőről, Haar Alfrédről, Kálmán Rudolfról, Lax Péterről, Radó Tiborról és Wintner Aurélról. Jelentős kutatóhelyei találhatók a Matematikai Kutató Intézetben, a BME-n, a szegedi JATE-n és a budapesti ELTE-n. A terület legelismertebb vezető kutatói Farkas Miklós és Hatvani László.

Radó Tibor (1895–1965) a konformis leképezések, a valós analízis, a variációszámítás, a parciális differenciálegyenletek, az integrálelmélet, topológia és matematikai logika területén kutatott. Nevéhez fűződik a Plateu-probléma megoldása és a felszíni mértékek elmélete. Ez utóbbi területen továbbfejlesztette Geőcze Zoárd eredményeit is.

Wintner Aurél (1903–1958) 1929-ben publikálta első könyvét Spektraltheorie unendlicher Matrizen címmel. Az analízis, számelmélet, differenciálegyenletek és valószínűségszámítás területén publikált jelentős eredményeket. Több közös dolgozata volt Norbert Wienerrel is. Henri Poincaréval és George David Birkhoffal az égi mechanika minden addiginál igényesebb matematikai megalapozását adta.

Erdélyi Artúr (1908–1977) a speciális függvények, különösen a hipergeometrikus függvények, az ortogonális polinomok és a Lamé-függvények vezető kutatója volt. Az aszimpotikus sorfejtések és szinguláris parciális differenciálegyenletek témakörét szintén vizsgálta. A Bateman-projekt keretében annak a csoportnak (Magnus, Oberhettinger, Tricomi) volt a vezetője, amelyik a Higher Transcedental Functions, 1–3. (1953) és a Tables of Integral Transforms, 1–2. (1954) c. könyveket írta. Ezek a munkák az alkalmazott matematikában és a fizikában a leggyakrabban idézett könyvek közé tartoznak és alapvető referenciáknak számítanak. További két jelentős könyve az Asymptotic expansions (1955) és az Operational Calculus and Generalised Functions (1962).

Lax Péter (1926–) fő kutatási területe a differenciálegyenletek és numerikus analízis.

A függvényegyenletek területén a magyar matematikusok jelentős eredményeket értek el, működésük nemzetközileg meghatározó a jelenben is. A függvényegyenletek megoldása az analízis egyik legrégibb problémaköre. Cauchy 1821-ben elsőként vizsgálta azt a kérdést, hogy milyen f(x) függvényekre teljesül azonosan az f(x+y)=f(x)+f(y) egyenlet minden valós x és y esetén. Az f(x) folytonosságának feltevésével igazolta, hogy f(x)=cx alakú, ahol c tetszőleges konstans. Némi egyszerűsítéssel a függvényegyenletek azt a kérdést vizsgálják, hogy egy adott egyenlet milyen függvényekre állhat fenn. A matematika, a közgazdaság, a fizika számos területén alkalmazott függvényegyenletek kutatását hazánkban elsőként Aczél János kezdeményezte, iskolákat hozott létre Miskolcon (Hosszú Miklós, Vincze Endre), Debrecenben és külföldön is. A debreceni iskola Daróczy Zoltán vezetésével a legjelentősebb kutatóközpontok egyike a világon. A számos fontos eredmény közül meg kell említeni Aczél János és Daróczy Zoltán közös monográfiáját (On measures of information and their characterization, 1975), amelyben az információelmélet sok kérdését sikerült tisztázni.

A magyar approximációelméleti iskola világhírét Fejér Lipót munkássága alapozta meg. Számos nevezetes eredményt ért el Haar Alfréd, Feldheim Ervin és Grünwald Géza is. Erdős Pál és Turán Pál jelentős, iskolateremtő munkássággal járult hozzá a terület fejlődéséhez. Itt kell megemlíteni Varga Richárd magyar származású amerikai matematikus jelentős hozzájárulását is a spline-approximációk és a racionális {IV-38.} approximációk területén. Ugyancsak figyelemre méltó eredményeket ért a külföldre távozott Névai Pál. Totik Vilmos a folytonossági modulus elméletében ért el kiemelkedő eredményeket. Jelentősebb approximációelméleti kutatások a Matematikai Kutató Intézetben és a szegedi JATE-n folynak.

Az ortogonális függvénysorok körében a magyarországi kutatásokat Fejér Lipót, Riesz Frigyes és Haar Alfréd indították el. Őket követte Csillag Pál, Fekete Mihály, Grünwald Géza és Sidon Simon. A II. világháború után jelentős tevékenységet fejtett ki Alexits György, aki a háború utáni iskola vezetője is volt, valamint Freud Géza, Leindler László, Móricz Ferenc, Schipp Ferenc és Tandori Károly. Jelenleg az ELTE-n és a JATE-n ténykednek jelentősebb kutatócsoportok.

Alexits György (1899–1978) a ponthalmazok elméletében, a metrikus geometriában, az ortogonális sorok elméletében, az approximációelméletben és a Bolyai-kutatásban ért el eredményeket. Az ortogonális sorok területén világviszonylatban vezető kutatónak számított. Fő műve a Konvergenzprobleme der Orthogonalreihen (1960).

A funkcionálanalízis területén a magyar hozzájárulás Riesz Frigyes munkásságával kezdődött. A területen dolgozó legjelentősebb magyar kutatók Halmos Pál, Neumann János és Szőkefalvi-Nagy Béla.

Halmos Pál (1916–) Véges dimenziós vektorterek (1942, magyarul 1984) c. könyvével egy csapásra híres matematikai író lett. Jelentős eredményeket ért el az operátorelmélet, az ergodelmélet, a funkcionálanalízis (különösen Hilbert-terek) területén. Magyarul is megjelent további művei: Elemi halmazelmélet (1981), Mértékelmélet (1984).

Topológiában az első hazai eredményt korát megelőzően Riesz Frigyes érte el. A témából az első könyvet Kőnig Dénes írta, majd őt követte Kerékjártó Béla. Jelentős eredményeket ért el Császár Ákos és Juhász István is. Császár Ákos (1924–) fő kutatási területe a valós függvénytan és az általános topológia. Legjelentősebb eredményeit topológiában érte el, ahol megteremtette és kidolgozta a szintopogén struktúrák elméletét. Általános topológiából két monográfiát: Fondaments de la Topologie générale (1960), Foundations of general topology (1963)) és egy tankönyvet: Bevezetés az általános topológiába (1970) írt.

Algebrai kutatások a Matematikai Kutató Intézetben, az ELTE-n, a JATE-n, a KLTE-n és a BME Matematikai Intézetében és más egyetemeken és főiskolákon is folynak. A századfordulón az algebra kutatása elsősorban a klasszikus algebrához és a határterületekhez (számelmélethez) kapcsolódott. 1920-tól az 1960-as évek elejéig az egyes struktúraosztályok kutatása állt előtérben, majd a hálóelméleti és az univerzális algebrai kutatások erősödtek fel. Kutatások folytak a félcsoportelméletben, a csoportelméletben, a gyűrűelméletben, a hálóelméletben, az univerzális algebrák elméletében, a lineáris algebra területén, a kategóriaelméletben, a klasszikus algebrában és az automataelméletben. A 20. század legelismertebb magyar algebrakutatói közé tartozik Kürschák József, Bauer Mihály, Rédei László, Szele Tibor, Kertész Andor, Fuchs László, Fried Ervin, Gratzer György, Schmidt Tamás és Wiegandt Richárd. A magyar algebrai iskola nemzetközileg elismert vezetője Rédei László volt.

Bauer Mihály (1874–1945) dolgozatai a számelmélet, az algebra, a függvénytan és a geometriai tárgykörében jelentek meg. Munkáira Ostrowski, Van der Waerden és Hasse több helyen is építettek.

Rédei László (1900–1980) számelmélettel (például a t2−du2=−1 alakú Pell-egyenlet megoldásával) és algebrával, félcsoportokkal, csoportokkal, gyűrűkkel és testekkel foglalkozott. Definiálta a csoportok egy igen általános ferde-szorzat {IV-39.} fogalmát, amely sok helyen (például a Burnside-sejtés megoldásában) gyümölcsözőnek bizonyult. Axiomatikus tárgyalást adott az euklideszi és nem-euklideszi geometriákra is. Algebra I. (1954) c. könyvét németre és angolra is lefordították. A hazai absztrakt algebra iskola létrehozója.

Szele Tibor (1918–1955) figyelemre méltó eredményeket ért el csoport- (Abel-csoportok) és gyűrűelméletben.

Kertész Andor (1929–1974) az Abel csoportok, modulusok és Artin gyűrűk területén kutatott. Híres monográfiája a Vorlesungen über artinische Ringe (1968), melyet angolra is lefordítottak.

A számelméletet már Bolyai János is művelte. A századfordulón Kőnig Gyulának, Rados Gusztávnak és Bauer Mihálynak volt e téren is jelentős munkássága. Erdős Pál és Turán Pál alapozták meg a hazai számelméleti iskolát. Rényi Alfréd különösen jelentős eredményeket ért el e területen is. Említést érdemel Rédei László, aki több dolgozatában foglakozott számelméleti kérdésekkel. A terület mai vezető kutatói többségükben Erdős, Turán és Rényi tanítványainak tekinthetők. A legjelentősebb számelméleti kutatók: Győry Kálmán, Halász Gábor, Kátai Imre, Ruzsa Z. Imre, Sárközy András és Pintz János. Számelméleti kutatások a Matematikai Kutató Intézetben és a tudományegyetemeken folynak. Különösen kiemelkedő eredményeket ért el a debreceni számelméleti iskola Győry Kálmán irányításával.

A halmazelmélet és matematikai logika, illetve a matematika alapjainak első nagy tudósai Kőnig Gyula és Neumann János voltak. Jelentős eredményeket ért el halmazelmélet kutatásában Erdős Pál, Fodor Géza és Hajnal András is. A hazai matematikai logikai kutatások legfontosabb vezetői Kalmár László és Péter Rózsa voltak. Meg kell még említeni Surányi János és Ruzsa Imre nevét is. Külföldön talán a legnevesebb magyar kutató Lakatos Imre volt. Fontos kutatások folytak a számítástudományi alkalmazásokkal (Prolog nyelv, k-értékű logika, relációs adatbázisok stb.) kapcsolatban is.

Kalmár László (1905–1976) az interpolációelmélet, a számelmélet, az algebra, absztrakt játékok elmélete és függvényegyenletek területén egyaránt végzett kutatásokat. Legfontosabb eredményeit a matematika alapjainak (matematika logika és halmazelmélet) vizsgálatában érte el. Új, algebrai módszerekre nem támaszkodó bizonyítást adott Post azon eredményére, miszerint az elemi logika aximatizálható. Kalmár egyszerűsített bizonyítást adott az eldöntésprobléma teljes megoldásának lehetetlenségére. Lényegesen egyszerűsítette Kurt Gödel azon híres tételének bizonyítását, amely szerint minden axiomatikusan megalapozott értelmes matematikai elméletben megfogalmazható olyan állítás, amelynek sem igaz volta, sem hamis volta nem bizonyítható a rendszer keretein belül maradva. Ugyancsak lényegesen egyszerűsítette Alonzo Church azon tételét, mely olyan végtelen probléma-sorozat létezését mondja ki, hogy egyfelől a problémasorozat leírható egységes eljárással, másfelől azonban nem létezik olyan egységes algoritmus, amely a problémák mindegyikét megoldaná. Sokat vizsgálta azt a Church által felvetett hipotézist, amely szerint pontosan azok az eljárások végezhetőek el, amelyeket általánosan-rekurzív algoritmusoknak neveznek. Kalmár megmutatta, hogy Church hipotézise olyan következményekhez vezet, amelyek elfogadhatatlanok. Fontos munkát végzett a számítástudomány és a számítógépek hazai meghonosításában, többek között formális nyelvekkel, önreprodukáló gépekkel foglalkozott. Leghíresebb eredménye a Kalmár-féle formulavezérlésű gép elve. Híresek a kollégáihoz írt ún. {IV-40.} Kalmár-levelek, a bennük foglalt nem publikált eredményeivel és problémafelvetéseivel is jelentős hatást gyakorolt a magyar matematikai életre. Szegeden létrehozta a kibernetikai laboratóriumot és elindította a programozó matematikusok képzését. Neve összeforrott a magyar számítástudomány és számítástechnika (informatika) megalapozásával.

Péter Rózsa (1905–1977) Kalmár László hatására a matematika alapjaival, a rekurzív függvények elméletével foglalkozott. Fő műve, a Rekursive Funktionen (1951) jelentős nemzetközi elismeréssel járt (angol, orosz és kínai nyelvre is lefordították). A Rekusive Funktionen in der Komputer-Theorie (1976) c. könyvében a rekurzív függvények elméletének számítástudományi alkalmazásait mutatja be. Világhírű népszerűsítő könyve a Játék a végtelennel (1944), amelyet tizenegy nyelven adtak ki.

Lakatos Imre (1922-1974) a matematikai logika területén ért el eredményeket. Munkájára Karl Popper és Pólya György voltak hatással. Híres munkája a Bizonyítások és cáfolatok (1976, magyarul 1981).

Fodor Géza (1927–1977) a stacionárius halmazok és a halmazleképezések elméletében ért el jelentős hatású eredményeket.

A geometriai kutatásokat a Bolyaiak neve fémjelzi. A kiegyezés utáni első geométerek még nem a Bolyaiak hatása alatt dolgoztak. A századfordulóra azonban a Bolyaiak munkáját már nagy mértékben feldolgozták, és a geometria alapjaival kapcsolatos kutatások szerepet kaptak a hazai matematikai életben is. Többek között Kerékjártó Béla, Rédei László és Szász Pál foglakoztak alapvető kutatásokkal. A geometriai szerkesztések elméletében Kürschák József és Szőkefalvi-Nagy Gyula ért el jelentős eredményeket. Magyar matematikusok fontos kutatásokat végeztek a differenciálgeometria és a diszkrét geometria területén. A magyar differenciálgeometriai iskolát Varga Ottó hozta létre, legerősebb kutató centruma a debreceni KLTE. A témában fontos eredményeket ért el Rapcsák András, Moór Arthur és Szenthe János. A diszkrét geometria jelentős mértékben magyar tudomány, létrehozásában oroszlánrésze van Fejes Tóth Lászlónak.

Szőkefalvi-Nagy Gyula (1887–1953) számelmélettel (diofantikus egyenletek), analízissel (polinomok geometriája, függvények zérushelyei) és geometriával foglalkozott. Fő műve A geometriai szerkesztések elmélete (1943).

Kerékjártó Béla (1898–1946) a topológia nemzetközi hírű kutatója volt. Fontos művei: Vorlesungen über Topologie (1923) és A geometria alapjai, 1–2. (1937, 1944).

Szász Pál (1901–1978) az analízís és főleg a geometria alapjai (Bolyai-geometria) körében végzett kutatásokat. Klasszikusnak számító munkája A differenciál- és integrálszámítás, 1–2. (1935, átdolgozott kiadás 1951). Jelentős műve a Bevezetés a Bolyai–Lobacsevszkij-féle geometriába (1973) is.

Varga Ottó

Varga Ottó (1909–1969) jelentős eredményeket ért el a differenciálgeometriában (Finsler-terek) és integrálgeometriában. A debreceni tudományegyetemen elindította a hazai differenciálgeometria-kutatásokat.

Rapcsák András (1914–1993) a Finsler-terek elméletében ért el eredményeket.

Fejes-Tóth László (1915–) fő kutatási területe a diszkrét geometria. A diszkrét geometriának mint önálló tudományágnak a megteremtése nagyrészt az ő nevéhez fűződik. Fő művei: Lagerungen in der Ebene, auf der Kugel und im Raum (1953), Regular Figures (1964).

A valószínűségszámítás és matematikai statisztika klasszikus elméletének kutatását Jordan Károly honosította meg Magyarországon. A modern értelemben vett kutatások és a hazai iskola megalapítása Rényi Alfréd nevéhez fűződik. {IV-41.} A terület első egyetemi tankönyvét is ő írta. Ugyancsak Rényi indította meg olyan speciális területek kutatását is mint a sztochasztikus folyamatok vagy az információelmélet. Az információelméletben Csiszár Imre, a sztochasztikus folyamatok kutatásában Arató Mátyás és Takács Lajos a legismertebb magyar matematikusok. Statisztikában Sarkadi Károly érte el a legnevesebb magyar eredményt (Sarkadi-féle normalitásvizsgálat). Jelentős volt a tudományterülethez a magyar származású Lukács Jenő és Wald Ábrahám hozzájárulása is. Valószínűségszámítási tanszék minden tudományegyetemen és a BME-n van. A Matematikai Kutató Intézetben több osztály is foglalkozik idevágó kutatásokkal.

Jordan Károly (1871–1959) tudományos munkássága a matematikán kívül kiterjedt a meteorológia, a geofizika és a kémia területére. Fő kutatási területe a valószínűségszámítás és a matematikai statisztika volt, amelyek hazai meghonosítása nevéhez fűződik. Egyéb kutatásai (differenciaszámítás, interpoláció) is ehhez kapcsolódtak. Nevezetes munkája a Fejezetek a klasszikus valószínűségszámításból (1956) c. könyv.

Lukács Jenő (1906–1987) valószínűségszámítással és matematikai statisztikával foglalkozott. Fontos műve a Characteristic Function Theory (1983).

Sarkadi Károly (1914–1985) matematikai statisztikai kutatásokat végzett. Leghíresebb eredménye a róla elnevezett Sarkadi-féle normalitásvizsgálat.

A kombinatorika és a gráfelmélet Kőnig Dénes, Erdős Pál és Turán Pál munkásságának köszönhetően nemcsak az újkori matematika fontos ágává vált, hanem speciális magyar kutatási területté is. A témakör legjelentősebb magyar művelői (a teljesség igénye nélkül): Babai László, Hajnal András, Katona Gyula, Lovász László, Szemerédi Endre, T. Sós Vera, Bollobás Béla. A neves amerikai kombinatorikus, Robert Endre Tarjan is magyar származású.

Kőnig Dénes (1884–1944) Kőnig Gyula fia. Gráfelméleti, halmazelméleti, geometriai és kombinatorikus topológiai témákkal foglalkozott. A felületek topológiájáról szóló könyve, Az analysis situs elemei (1918) a nemzetközi irodalomban is az első volt a tárgykörben. Az ő munkássága révén vált a gráfelmélet a matematika fontos, új fejezetévé. Számos alapvető gráfelméleti tétel fűződik nevéhez. A legjelentősebb hatást Theorie der endlichen und unendlichen Graphen (1936) c. könyve gyakorolta, amely 1958-ig az egyetlen gráfelméleti könyv volt. Egyik tételének Egervárytól származó bizonyítása és általánosítása, a Kőnig–Egerváry tétel, Kuhn amerikai matematikust a „magyar módszer” néven ismert fontos operációkutatási eljárás kidolgozására inspirálta.

A számítástudomány úttörője Neumann János volt. A hazai számítástudományi kutatások az 1960-as években indultak meg. Jelentős munkát végzett e téren Kalmár László, ide tartozik részben Péter Rózsa munkássága is. Az automataelmélet területén Gécseg Ferenc irányításával Szegeden nemzetközileg elismert műhely alakult ki. Az adatbázisok témakörben Demetrovics János és Benczúr András ért el kiemelkedő eredményeket. Ugyancsak kiemelkedő eredményeket értek el a számítástudomány sztochasztikus problémáinak vizsgálatában Arató Mátyás és tanítványai. Jelentősebb számítástudományi kutatások az ELTE-n, a JATE-n, a KLTE-n, a BME-n és az MTA SzTAKI-ban folynak. Ki kell emelni, hogy Szegeden a számítástudomány kutatását Kalmár László honosította meg. A magyar származású Kemény János György nevéhez fűződik a BASIC programozási nyelv kifejlesztése.

Kemény János György (1926–1992) Thomas Kurtzzal kidolgozta a BASIC programozási nyelvet. Kezdeményezte a véges matematikának az oktatásba történő bevezetését. Társszerzője volt A modern {IV-42.} matematika alapjai (véges struktúrák) (1957, magyarul 1971) c. könyvnek. Ismert műve Az ember és a számítógép (1972, magyarul 1978) is.

Az alkalmazott matematikának kevés híres magyar művelője van, annak ellenére, hogy a századforduló körül tevékenykedő matematikusaink közül Vályi Gyula, Réthy Mór és Farkas Gyula is alkalmazott matematikai kérdésekkel foglalkozott. Ennek oka talán az, hogy Magyarországon az ipari-gazdasági háttér soha sem volt olyan kedvező mint az ipari nagyhatalmak esetében. Mindennek ellenére volt néhány világhírű matematikus ezen a területen is. Kármán Tódor az áramlástanban, Lánczos Kornél a fizikában és a numerikus analízisben alkotott kiválót. Neumann János a kvantumfizika, a lökéshullámok, a meteorológia, a játékelmélet és a numerikus analízis területén ért el kimagasló eredményeket. A numerikus matematika jelentős magyar származású kutatója Lax Péter és Varga Richárd. Az itthon működő neves alkalmazott matematikusok közül Jordan Károly és Egerváry Jenő nevét kell említeni. A számítástechnika elterjedésével párhuzamosan Magyarországon is létrejött egy erős operációkutatási iskola Prékopa András vezetésével, aki jelentős eredményeket ért el a sztochasztikus programozás területén. Az operációkutatást minden egyetemen tanítják. Tanszéke van az ELTE Természettudományi Karán, a Budapesti Közgazdaság-tudományi Egyetemen és a pécsi Janus Pannonius Tudományegyetemen. Jelentős kutatócsoport működik az MTA SzTAKI-ban. Az alkalmazott matematikához tartozó egyéb területek közül a numerikus analízisnek van tanszéke az ELTE-n. Alkalmazott matematikai tanszék Debrecenben és Miskolcon is működik.

Kármán Tódor (1881–1963) 1911-ben tette nagy felfedezését a később róla elnevezett Kármán-féle örvények leírásával. Az I. világháborúban katonai szolgálat keretében Bécsben részt vett az első helikopter fejlesztésében. Fontos szerepe volt az USA repülő- és rakétafejlesztéseiben, a kutatóhálózat kialakításában. Fő kutatási területei az áramlástan, a turbulencia elmélete, a szuperszonikus repülés elmélete, a parciális differenciálegyenletek, a matematika alkalmazása a mérnöki tudományokban, a repülőgép szerkezetekben és a talajmechanikában. Önéletrajza magyarul is megjelent: Örvények és repülők: Kármán Tódor élete és munkássága (1994). Híres alkalmazott matematikai munkája a Matematikai módszerek műszaki feladatok megoldására (társszerző M. A. Biot, magyarul 1963) c. könyv.

Egerváry Jenő (1891–1958) tudományos kutatásait az analízis, a differenciálegyenletek, a geometria (vektoranalízis), a lineáris algebra és alkalmazások körében végezte. Az analízisben az integrálegyenletek, a hatványsorok, a polinomok geometriája, valamint a stabil interpoláció körében Turán Pállal elért eredményei sok esetben Fejér Lipót munkásságához kapcsolódnak. A differenciálegyenletek körében elsősorban a háromtest problémával, a hővezetéssel és az elektronmozgás differenciálegyenleteivel foglalkozott. A lánchidak elméletét, valamint Turán Pállal közösen a kinetikus gázelmélet alapjait is tanulmányozta. Legismertebb eredményeit a lineáris algebra területén érte el. Itt a diadikus felbontásra támaszkodva egy általános rangszámcsökkentő eljárást adott mátrixok bázisfaktorizációjára, amelynek segítségével több jelentős eredményt (Stieltjes-lemma általánosítása, mátrixok különféle szorzatfelbontásai, Jordan-féle normálalak előállítása) ért el. A rangszámcsökkentő eljárás segítségével több egyenletrendszer-megoldó algoritmust javasolt és megmutatta ennek meglepő kapcsolatát ismert konjugált irány módszerekkel. A rangszámcsökkentő eljárás egy az 1980-as években kifejlesztett új egyenletrendszer megoldó módszercsalád {IV-43.} (ABS-módszerek) alapját képezte. Leghíresebb eredménye Kőnig Dénes egy gráfelméleti eredményéhez kapcsolódik. Bármely mátrixra az olyan vonalak (azaz sorok és oszlopok) minimális száma, amelyek összességükben az összes el nem tűnő elemeket tartalmazzák, megegyezik az olyan el nem tűnő elemek maximális számával, amelyek páronként nem feküsznek egy vonalban. Egerváry e tétel új bizonyítását és általánosítását adta. Ez a következőt mondja ki: válasszunk ki a nem negatív egész elemekből álló n-edrendű 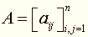mátrixból n elemet: 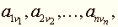amelyek kettesével más-más sorba és más-más oszlopba tartoznak, és legyen M az összes így adódó 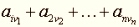összegek maximális értéke. Legyenek másrészt λ1,λ2,…,λn, μ1,μ2,…,μn olyan nem negatív egész számok, amelyek i,j=1,2,…,n-re kielégítik a λi+μj≥aij feltételeket. Akkor a λ1+μ1+λ2+μ2+…+λn+μn összeg legkisebb értéke éppen M. (Kőnig tétele abban az esetben adódik, amikor minden aij vagy 0 vagy 1.) Kuhn amerikai matematikus ezt az eredményt használta fel a „hozzárendelési probléma” megoldására, amelyet Kőnig és Egerváry tiszteletére „magyar módszernek” nevezett. Később Egerváry a módszert az amerikai eredmények ismeretében a szállítási probléma megoldására alkalmazta.